
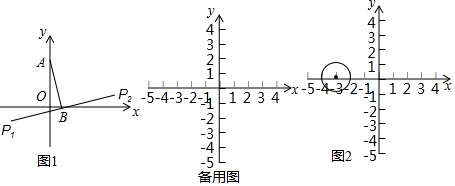
分析 (1)①根据全等三角形即可解决问题;
②如图2中,取N(4,0),则OA=ON,作P1M⊥x轴于M,首先说明P1的运动轨迹是一条直线,求出这条直线的解析式即可解决问题;
(2)利用(1)②的结论,A(0,m)关于B的“伴随点”P(x,y),y与x之间的关系式:y=x-m或y=-x-m,由题意可知,当直线y=x-m或y=-x-m与⊙C有交点时,在⊙C上存在点A关于点B的“伴随点”,求出这两条直线和⊙C相切时的m的值,即可解决问题;
解答 解:(1)①如图1中,作P1M⊥x轴于M.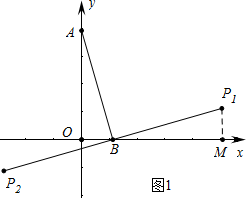
∵AB=BP1,∠AOB=∠P1MB=90°,易证∠ABO=∠P1,
∴△ABO≌△BP1M,
∴OA=BM,OB=P1M,
当A(0,4),B(1,0)时,BM=4,P1M=1,OM=5,
∴P1(5,1),
∵P2与P1关于B对称,
∴P2(-3,-1),
当A(0,4),B(-2,0)时,同法可得P1(2,-2),P2(-6,2),
故答案为(5,1),(-3,-1)和(2,-2),(-6,2)
②如图2中,取N(4,0),则OA=ON,作P1M⊥x轴于M.
∵△ABO≌△BP1M,
∴OA=BM=ON,OB=P1M,
∴OB=MN=P1M,
∴△P1MN是等腰直角三角形,
∴∠P1NM=45°,
∴点P1在经过点N,与x轴的夹角为45°的直线上,
易知这条直线的解析式为y=x-4,
∴P1(x,y)是点A关于点B的“伴随点”,y与x之间的关系式为y=x-4,
同法可得P2(x,y),在直线y=-x-4,
∴y与x之间的关系式:y=x-4或y=-x-4.
(2)如图3中,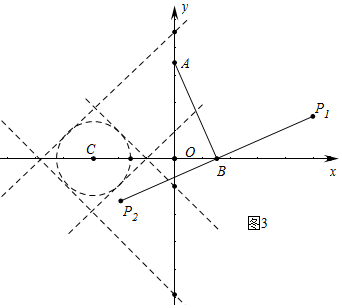
由(1)可知,A(0,m)关于B的“伴随点”P(x,y),
y与x之间的关系式:y=x-m或y=-x-m,
由题意可知,当直线y=x-m或y=-x-m与⊙C有交点时,在⊙C上存在点A关于点B的“伴随点”,
易知相切时m=±1或±5,
观察图象可知,满足条件的m的范围为:-5≤m≤-1或1≤m≤5.
点评 本题考查圆综合题、一次函数的解析式、切线的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,本题的突破点是发现点P的运动轨迹是直线,题目比较难,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
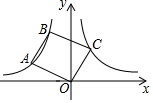 如图,点A、B在双曲线y=$\frac{3}{x}$(x<0)上,连接OA、AB,以OA、AB为边作?OABC.若点C恰落在双曲线y=$\frac{2}{x}$(x>0)上,此时?OABC的面积为2$\sqrt{7}$.
如图,点A、B在双曲线y=$\frac{3}{x}$(x<0)上,连接OA、AB,以OA、AB为边作?OABC.若点C恰落在双曲线y=$\frac{2}{x}$(x>0)上,此时?OABC的面积为2$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是一局围棋比赛的几手棋,为记录棋谱方便,横线用数字表示,纵线也用数字表示,这样,黑棋
如图是一局围棋比赛的几手棋,为记录棋谱方便,横线用数字表示,纵线也用数字表示,这样,黑棋 的位置可记为(2,2),白棋②的位置可记为(4,1),则白棋⑨的位置应记为( )
的位置可记为(2,2),白棋②的位置可记为(4,1),则白棋⑨的位置应记为( )| A. | (3,5) | B. | (3,4) | C. | (4,3) | D. | (5,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com