练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．圆的周长公式为C=2πr，下列说法正确的是（　　）
    A．常量是2B．变量是C、π、rC．变量是C、rD．常量是2、r

    分析 根据函数的定义：对于函数中的每个值x，变量y按照一定的法则有一个确定的值y与之对应；来解答即可．

    解答 解：圆的周长公式为C=2πr，
    变量是C、r，常量是2、π，故C正确；
    故选：C．

    点评 本题考查了常量与变量，函数的定义：设x和y是两个变量，D是实数集的某个子集，若对于D中的每个值x，变量y按照一定的法则有一个确定的值y与之对应，称变量y为变量x的函数，记作y=f（x）；变量是指在程序的运行过程中随时可以发生变化的量．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．如图，已知两个正方形全等，证明：HL=MJ，MJ⊥HL．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，已知⊙O1与⊙O2相交于A，B两点，AB是⊙O2的直径，过A点作⊙O1的切线交⊙O2于点E，并与BO1的延长线交于点P，PB分别与⊙O1，⊙O2交于C，D两点，求证：
    （1）PA•PD=PE•PC；
    （2）AD=AE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．若x，y，z满足$\left\{\begin{array}{l}{2x+3y-5z=0}\\{4x-y-3z=0}\end{array}\right.$，且xyz≠0，则$\frac{2x-3y}{4y+2z}$=-$\frac{1}{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知x-3$\sqrt{xy}$-4y=0，则$\frac{2x+3\sqrt{xy}-2y}{3x-\sqrt{xy}+y}$=$\frac{14}{15}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列多项式中，分解因式后含有因式（a+3）的是（　　）
    A．a2-6a+9B．a2+2a-3C．a2-6D．a2-3a

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．观察下列数，按规律填空．
    1，-$\frac{1}{3}，\frac{1}{5}，-\frac{1}{7}$，$\frac{1}{9}$，$-\frac{1}{11}$，$\frac{1}{13}$，第2015个数是$\frac{1}{2015}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

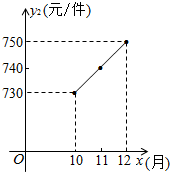    3．某企业为重庆计算机产业基地提供电脑配件．受美元走低的影响，从去年1至9月，该配件的原材料价格一路攀升，每件配件的原材料价格y1（元）与月份x（1≤x≤9，且x取整数）之间的函数关系如下表：
    月份x123456789
    价格y1（元/件）560580600620640660680700720
    随着国家调控措施的出台，原材料价格的涨势趋缓，10至12月每件配件的原材料价格y2（元）与月份x（10≤x≤12，且x取整数）之间存在如图所示的变化趋势：
    （1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y1 与x之间的函数关系式，根据如图所示的变化趋势，直接写出y2与x之间满足的一次函数关系式；
    （2）若去年该配件每件的售价为1000元，生产每件配件的人力成本为50元，其它成本30元，该配件在1至9月的销售量p1（万件）与月份x满足关系式p1=0.1x+1.1（1≤x≤9，且x取整数），10至12月的销售量p2（万件）p2=-0.1x+2.9（10≤x≤12，且x取整数）．求去年哪个月销售该配件的利润最大，并求出这个最大利润；
    （3）今年1至5月，每件配件的原材料价格均比去年12月上涨60元，人力成本比去年增加20%，其它成本没有变化，该企业将每件配件的售价在去年的基础上提高a%，与此同时每月销售量均在去年12月的基础上减少0.1a%．这样，在保证每月上万件配件销量的前提下，完成1至5月的总利润1700万元的任务，请你参考以下数据，估算出a的整数值．（参考数据：992=9801，982=9604，972=9409，962=9216，952=9025）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．解方程组 
    （1）$\left\{\begin{array}{l}{3x-2y=6}\\{2x+3y=17}\end{array}\right.$               
    （2）$\left\{\begin{array}{l}{\frac{x+y}{2}+\frac{x-y}{2}=6}\\{4（x+y）-5（x-y）=2}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案