
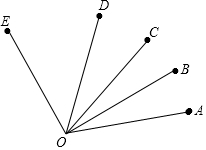
 已知:如图,线段OA、OB、OC、OD、OE在同一平面内,且∠AOE=110°,∠AOB=20°.
已知:如图,线段OA、OB、OC、OD、OE在同一平面内,且∠AOE=110°,∠AOB=20°.分析 (1)由OB平分∠AOC,可得∠AOC=2∠AOB=40°,那么∠COE=∠AOE-∠AOC=70°;
(2)先求出∠BOE=∠AOE-∠AOB=90°,再根据角平分线定义得出∠BOD=$\frac{1}{2}$∠BOE=45°,∠BOC=∠AOB=20°,代入∠COD=∠BOD-∠BOC即可求解;
(3)设经过x分钟,OA与OB第一次垂直.根据OA与OB第一次垂直时,分针比时针多转110°列出方程6x-$\frac{1}{2}$x=90+20,求解即可.
解答 解:(1)∵OB平分∠AOC,∠AOB=20°,
∴∠AOC=2∠AOB=40°,
∵∠AOE=110°,
∴∠COE=∠AOE-∠AOC=70°;
(2)∵∠AOE=110°,∠AOB=20°,
∴∠BOE=∠AOE-∠AOB=90°,
∵OD平分∠BOE,OB平分∠AOC,
∴∠BOD=$\frac{1}{2}$∠BOE=45°,∠BOC=∠AOB=20°,
∴∠COD=∠BOD-∠BOC=25°;
(3)设经过x分钟,OA与OB第一次垂直.
由题意得,6x-$\frac{1}{2}$x=90+20,解得 x=20.
答:经过20分钟,OA与OB第一次垂直.
点评 本题考查了角的计算,角平分线定义,一元一次方程的应用,掌握角平分线定义、准确识图以及追击问题的相等关系是解题的关键.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
| 时间t/天 | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y/千克 | 118 | 114 | 108 | 100 | 80 | 40 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
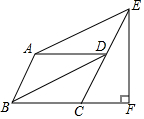 如图,在?ABCD中,∠BCD=120°,连接BD,过点A作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB=2.
如图,在?ABCD中,∠BCD=120°,连接BD,过点A作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
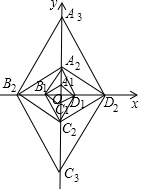 已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1、B1D1相交于点O,以点O为坐标原点,分别以OB1,OA1所在直线为x轴、y轴建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在y轴的正半轴上得到点A1,A2,A3,…,An,则点A2017的坐标为(0,32016).
已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1、B1D1相交于点O,以点O为坐标原点,分别以OB1,OA1所在直线为x轴、y轴建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在y轴的正半轴上得到点A1,A2,A3,…,An,则点A2017的坐标为(0,32016).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com