
如图,将一张长方形纸片对折,然后剪下一个角,如果剪出的角展开后是一个直角,那么剪口线与折痕AB形成的夹角度数是( )

A. 180° B. 90° C. 45° D. 22.5°
C 【解析】试题分析:根据折叠图形的性质可知:剪口线与折痕AB形成的夹角的度数=90°÷2=45°,故选择C.科目:初中数学 来源:2017-2018学年北师大版七年级数学上册:第5章 一元一次方程 单元测试卷 题型:单选题
某班分两组去两处植树,第一组22人,第二组26人.现第一组在植树中遇到困难,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程( )
A. 22+x=2×26
B. 22+x=2(26-x)
C. 2(22+x)=26-x
D. 22=2(26-x)
B 【解析】设第二组调到第一组x人,则第一组的现有人数为:(22+x)人,第二组的现有人数为:(26-x)人,又由于第一组现有人数是第二组的2倍,因此可列方程为: 22+x=2(26-x),故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县九年级(上)期末数学试卷(五四学制) 题型:填空题
抛物线y=x2+8x﹣4与直线x=﹣4的交点坐标是_____.
(﹣4,﹣20) 【解析】试题解析:∵当x=-4时,y=(-4)2+8×(-4)-4=-20, ∴抛物线y=x2+8x-4与直线x=-4的交点坐标是(-4,-20). 故答案为:(-4,-20).查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第4章 基本平面图形 单元测试卷 题型:填空题
已知A、B、C是直线l上的三点,且线段AB=9cm,BC= AB,那么A、C两点的距离是____________.
AB,那么A、C两点的距离是____________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第4章 基本平面图形 单元测试卷 题型:单选题
如图,点C在线段AB上,点D是AC的中点,如果CD=3cm,AB=10cm,那么BC的长度是( )

A. 3cm B. 3.5cm C. 4cm D. 4.5cm
C 【解析】试题分析:根据线段中点的定义求出AC,再根据BC=AB﹣AC计算即可得解. 【解析】 ∵点D是AC的中点, ∴AC=2CD=2×3=6cm, ∴BC=AB﹣AC=10﹣6=4cm. 故选C.查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:解答题
甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
(1)甲的平均攀登速度是12米/分钟;(2)倍. 【解析】试题分析:(1)根据题意可以列出相应的分式方程,从而可以求得甲的平均攀登速度; (2)根据(1)中甲的速度可以表示出丙的速度,再用甲的速度比丙的平均攀登速度即可解答本题. 试题解析::(1)设乙的速度为x米/分钟, , 解得,x=10, 经检验,x=10是原分式方程的解, ∴1.2x=12, ...查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:填空题
如图,点P是∠AOB内部的一点,∠AOB=30°,OP=8 cm,M,N是OA,OB上的两个动点,则△MPN周长的最小值_____cm.

查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:解答题
如图,直线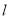 :
:  与
与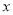 轴、
轴、 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线 与
与 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥ 轴交
轴交 于点D,PE∥
于点D,PE∥ 轴交
轴交 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十八章达标检测卷 题型:单选题
下列命题中,真命题是( )
A. 有两边相等的平行四边形是菱形 B. 对角线垂直的四边形是菱形
C. 四个角相等的菱形是正方形 D. 两条对角线相等的四边形是矩形
A 【解析】试题分析:A.反例:等腰梯形;B.反例:风筝型;D.反例:等腰梯形 故选C查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com