

���� ��1����ADFΪֱ�������Σ������ֿ��ܣ���ADF=90����AFD=90�㣬����������Ǻ����з�����⼴�ɣ�
��2���ٸ������ε��ж�����֪��AD=DFʱ���ı���ADFD��Ϊ���Σ�����������Ǻ����з������x���������ε�������ɣ�
�ڸ���������Ǻ�����ʾ��AG��D��G��GE�����ݹ��ɶ����г���������ʽ��
�۸�����������λ�߶�����֪�߶�MNɨ�����������״��ƽ���ı��Σ������Ϊ$\frac{24}{5}$��
��� �⣺��1���ߡ�ACB=90�㣬BC=8��tanA=$\frac{4}{3}$��
��BC=8��AB=10��
��AD=x��BE=x��AF=6-x��
����ADF=90�㣬��ͼ1��ͼ��
��tanA=$\frac{4}{3}$��
��cosA=$\frac{3}{5}$��
��$\frac{AD}{AF}=\frac{x}{6-x}=\frac{3}{5}$��
��$x=\frac{9}{4}$��
����AFD=90�㣬��ͼ1��ͼ��
��tanA=$\frac{4}{3}$
��cosA=$\frac{3}{5}$��
��$\frac{AF}{AD}=\frac{6-x}{x}=\frac{3}{5}$��
��$x=\frac{15}{4}$��
�൱$x=\frac{9}{4}$��$x=\frac{15}{4}$����ADFΪֱ�������Σ� ��2������ͼ2��
��2������ͼ2��
��AD=AD�䣬D��F=DF��
�൱AD=DFʱ���ı���ADFD��Ϊ���Σ�
������DD���AF��G��AG=$\frac{6-x}{2}$��
��tanA=$\frac{4}{3}$
��cosA=$\frac{3}{5}$��
��$\frac{AG}{AD}=\frac{{\frac{6-x}{2}}}{x}=\frac{3}{5}$��
��x=$\frac{30}{11}$��
S����=$\frac{1}{2}��DD'��AF=\frac{1}{2}��\frac{48}{11}��\frac{36}{11}=\frac{864}{121}$�� ����ͼ3����D��G��AF��G��
����ͼ3����D��G��AF��G��
��tanA=$\frac{4}{3}$��
��cosA=$\frac{3}{5}$��sinA=$\frac{4}{5}$��
��$AG=\frac{3}{5}x��D'G=\frac{4}{5}x$
��$GE=10-x-\frac{3}{5}x=10-\frac{8}{5}x$��
��$y=\sqrt{{{��10-\frac{8}{5}x��}^2}+{{��\frac{4}{5}x��}^2}}=\sqrt{\frac{16}{5}{x^2}-32x+100}$=2$\sqrt{\frac{4}{5}{x}^{2}-8x+25}$��
��3��ƽ���ı��Σ�$\frac{24}{5}$��
��M��N�ֱ�ΪD��F��D��E���е㣬
��MN��EF��MN=$\frac{1}{2}$EF=2��
���߶�MNɨ�����������״��ƽ���ı��Σ�
��D�˶���C����F�����˶���A����ʱMA=$\frac{1}{2}$D��A=$\frac{1}{2}$DA=3��
�ߡ�DAB=��D��AB��
��tanA=tan��D��AB=$\frac{4}{3}$��
��M��AB�ľ�����Ϊ4x����3x��2+��4x��2=32��
��ã�x=$\frac{3}{5}$��
4x=$\frac{12}{5}$��
���߶�MNɨ�����������״��ƽ���ı��ε����=2��$\frac{12}{5}$=$\frac{24}{5}$��
���� ������Ҫ������������Ǻ�����ֱ�������ε��ж������ε��ж������ɶ����Լ���������λ�����ʵ��ۺ����ã��߱���ǿ�����ν�������ǽ������Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭��ʡ���꼶��ѧ�ڵ�һ�ο��õ�����ѧ�Ծ��������棩 ���ͣ���ѡ��
��1���2��һ��ƽ���߱�������ֱ�����ص�ͬ���ڽǣ�����1=50�㣬�� ��
A. ��2=50�� B. ��2=130�� C. ��2=50����2=130�� D. ��2�Ĵ�С��һ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ֱ������ϵ�У�����OABC�ı�OA��x���������ϣ���OC��y����������ϣ�B�������Ϊ��4��8����������OABC�Ƶ�B��ʱ����ת�õ�����EFBG����Eǡ������x���ϣ�
��ͼ����֪��ֱ������ϵ�У�����OABC�ı�OA��x���������ϣ���OC��y����������ϣ�B�������Ϊ��4��8����������OABC�Ƶ�B��ʱ����ת�õ�����EFBG����Eǡ������x���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ�������У�����A��4��0����������y=-x2+bx��ֱ��y=-x+b������һ��B����������y=-x2+bx�Ķ���E��EF��x����F�㣬��M��t��d��Ϊ������y=-x2+bx��x���Ϸ��Ķ��㣮
��ͼ����ƽ��ֱ�������У�����A��4��0����������y=-x2+bx��ֱ��y=-x+b������һ��B����������y=-x2+bx�Ķ���E��EF��x����F�㣬��M��t��d��Ϊ������y=-x2+bx��x���Ϸ��Ķ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
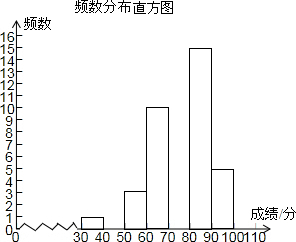 ��ͼ��ijУΪ�˽���꼶300��ѧ�����п�����ѧ�ɼ����������˸��꼶50��ѧ�������п���ѧ�ɼ����з����������˲�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
��ͼ��ijУΪ�˽���꼶300��ѧ�����п�����ѧ�ɼ����������˸��꼶50��ѧ�������п���ѧ�ɼ����з����������˲�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��| �ɼ����� | Ƶ�� | Ƶ�� |
| 30��x��40 | 1 | 0.02 |
| 40��x��50 | 1 | 0.02 |
| 50��x��60 | 3 | 0.06 |
| 60��x��70 | 10 | 0.2 |
| 70��x��80 | 15 | 0.3 |
| 80��x��90 | 15 | 0.3 |
| 90��x��100 | 5 | 0.1 |
| �ϼ� | 50 | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ʵʩ���ʽ���������ij��ѧ������ѧ����������չ�����������γ���Դ�������꼶������������ѧϰС�飬���������꼶ѧ���μ�����ѧϰС���ͳ�Ʊ�������ͳ��ͼ���������ͼ�����ṩ����Ϣ�ش��������⣮
ʵʩ���ʽ���������ij��ѧ������ѧ����������չ�����������γ���Դ�������꼶������������ѧϰС�飬���������꼶ѧ���μ�����ѧϰС���ͳ�Ʊ�������ͳ��ͼ���������ͼ�����ṩ����Ϣ�ش��������⣮| ѧϰС�� | ���� | ���� | �Ƽ� | ���� | д�� | ���� |
| ���� | 72 | 36 | 54 | 18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com