
【题目】如图,已知,A、O、B在同一条直线上,∠AOE=∠COD,∠EOD=30°.
(1)若∠AOE=88°30′,求∠BOC的度数;
(2)若射线OC平分∠EOB,求∠BOC的度数.

【答案】(1) 33°;(2) ∠BOC=50°
【解析】
(1)先求出∠AOC度数,再利用∠AOC与∠BOC互补关系求解;
(2)由∠AOE=∠COD,易得∠AOD=∠COE,再借助角平分线定义分析出∠AOD=∠COE=∠BOC,根据这三个等角加上∠DOE等于180°列方程,从而可求出∠BOC度数.
(1)∵∠AOC=∠AOE+∠DOC-∠DOE =88°30′+88°30′-30°=147°,
∴∠BOC=180°-∠AOC =180°-147°=33°;
(2)∵∠AOE=∠COD,
∴∠AOE-∠DOE=∠COD-∠DOE,
即∠AOD=∠COE,
∵OC平分∠BOE,
∴∠BOC=∠COE,
∴∠BOC=∠COE=∠AOD,
设∠BOC=∠COE=∠AOD=x°,
则3x+30°=180°,解得x=50°,
所以∠BOC=50°.


科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OM⊥AB.
(1)∠AOC的邻补角为 (写出一个即可);
(2)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(3)若∠1=![]() ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图: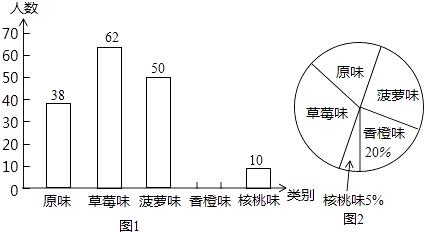
(1)本次被调查的学生有名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察一列数:1,2,4,8,16,…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列3,-12,48,…的第4项是______;
(2)如果一列数a1,a2,a3,a4,…是等比数列,且公比为q.那么有:a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3,则a5=_______,an=______(用a1与q的式子表示);
(3)一个等比数列的第2项是9,第4项是36,求它的公比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.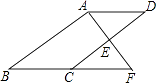
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
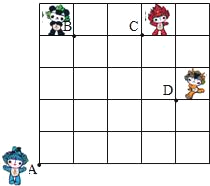
【题目】如图,奥运福娃在5×5的方格(每个格边长尾1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:
B→A(﹣4,﹣1).请根据图中所给信息解决下列问题:
(1)A→C(______),_____);
B→C(______),_____);C→_____(﹣4,﹣3);
(2)如果贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)如果贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),
(+2,﹣1),(﹣2,+3),(﹣1,﹣1),请在图中标出妮妮的位置E点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形ABD中,∠A=90°,AB=AD=2,作△ABD关于直线BD对称的△CBD,已知点F为线段AB上一点,且AF=m,连接CF,作∠FCE=90°,CE交AD的延长线于点E.
(1)求证:△BCF≌△DCE;
(2)若AE=n,且mn=3,求m2+n2的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com