
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.
(1)求a,c的值;
(2)连结OF,试判断△OEF是否为等腰三角形,并说明理由;
(3)现将一足够大的三角板的直角顶点Q放在射线AF或射线HF上,一直角边始终过点E,另一直角边与y轴相交于点P,是否存在这样的点Q,使以点P,Q,E为顶点的三角形与△POE全等?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵△ABC为等腰直角三角形,
∴OA= ![]() BC.
BC.
又∵△ABC的面积= ![]() BC×OA=4,即OA2=4,
BC×OA=4,即OA2=4,
∴OA=2.
∴A(0,2),B(﹣2,0),C(2,0).
∴ ![]() ,
,
解得:  .
.
(2)
解:△OEF是等腰三角形.理由如下:如答图1,
∵A (0,2)),B (﹣2,0),
∴直线AB的函数表达式为:y=x+2,
又∵平移后的抛物线顶点F在射线BA上,
∴设顶点F的坐标为(m,m+2).
∴平移后的抛物线函数表达式为:y=﹣ ![]() (x﹣m)2+m+2.
(x﹣m)2+m+2.
∵抛物线过点C (2,0),
∴﹣ ![]() (x﹣m)2+m+2=0,解得m1=0,m2=6.
(x﹣m)2+m+2=0,解得m1=0,m2=6.
∴平移后的抛物线函数表达式为:y=﹣(x﹣6)2+8,
即y=﹣ ![]() x2+6x﹣10.
x2+6x﹣10.
当y=0时,﹣ ![]() x2+6x﹣10=0,
x2+6x﹣10=0,
解得x1=2,x2=10.
∴E(10,0),OE=10.
又∵F(6,8),OH=6,FH=8.
∴OF= ![]() =
= ![]() =10,
=10,
∴OE=OF,即△OEF为等腰三角形.

(3)
解:存在点Q(6,2 ![]() )或(6,3)或(10,12)或(4+
)或(6,3)或(10,12)或(4+ ![]() ,6+
,6+ ![]() )或(4﹣
)或(4﹣ ![]() ,6﹣
,6﹣ ![]() ),使以P,Q,E三点为顶点的三角形与△POE全等.
),使以P,Q,E三点为顶点的三角形与△POE全等.
理由如下:
点Q的位置分两种情形:
情形一:点Q在射线HF上,
当点P在x轴上方时,如答图2.
∵△PQE≌△POE,
∴QE=OE=10.
在Rt△QHE中,QH= ![]() =
= ![]() =2
=2 ![]() ,
,
∴Q(6,2 ![]() ).
).
当点P在x轴下方时,如答图3,有PQ=OE=10,
过P点作PK⊥HF于点K,则有PK=6.
在Rt△PQK中,QK= ![]() =
= ![]() =8,
=8,
∵∠PQE=90°,
∴∠PQK+∠HQE=90°.
∵∠HQE+∠HEQ=90°,
∴∠PQK=∠HEQ.
又∵∠PKQ=∠QHE=90°,
∴△PKQ∽△QHE.
∴ ![]() ,
,
即 ![]() ,
,
解得QH=3.
∴Q(6,3).
情形二:点Q在射线AF上,
当PQ=OE=10时,如答图4,有QE=PO,
∴四边形POEQ为矩形,
∴Q的横坐标为10.
当x=10时,y=x+2=12,
∴Q(10,12).
当QE=OE=10时,如答图5.
过Q作QM⊥y轴于点M,过E点作x轴的垂线交QM于点N,
设Q的坐标为(x,x+2),
∴MQ=x,QN=10﹣x,EN=x+2.
在Rt△QEN中,有QE2=QN2+EN2,
即102=(10﹣x)2+(x+2)2,
解得:x=4± ![]() .
.
当x=4+ ![]() 时,如答图5,y=x+2=6+
时,如答图5,y=x+2=6+ ![]() ,
,
∴Q(4+ ![]() ,6+
,6+ ![]() ).
).
当x=4﹣ ![]() 时,如答图6,y=x+2=6﹣
时,如答图6,y=x+2=6﹣ ![]() ,
,
∴Q(4﹣ ![]() ,6﹣
,6﹣ ![]() ).
).
综上所述,存在点Q(6,2 ![]() )或(6,3)或(10,12)或(4+
)或(6,3)或(10,12)或(4+ ![]() ,6+
,6+ ![]() )或(4﹣
)或(4﹣ ![]() ,6﹣
,6﹣ ![]() ),使以P,Q,E三点为顶点的三角形与△POE全等.
),使以P,Q,E三点为顶点的三角形与△POE全等.





【解析】(1)由△ABC为等腰直角三角形,且面积为4,易求得OA的长,即可求得点A,B,C的坐标,然后由待定系数法求得答案;(2)首先求得直线AB的函数表达式,设顶点F的坐标为(m,m+2),由抛物线过点C (2,0),可求得平移后的抛物线函数表达式,继而求得点E的坐标,即可判定△OEF是等腰三角形;(3)分别情形一:从点Q在射线HF上,当点P在x轴上方时或当点P在x轴下方时,以及情形二:点Q在射线AF上,去分析求解即可求得答案.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°. 
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径长为1,求由弧BC、线段CD和BD所围成的阴影部分面积.(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AC=BC=10,AB=12.
(1)动手操作:利用尺规作以BC为直径的⊙O,⊙O交AB于点D,⊙O交AC于点E,并且过点D作DF⊥AC交AC于点F.
(2)求证:直线DF是⊙O的切线;
(3)连接DE,记△ADE的面积为S1 , 四边形DECB的面积为S2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ADB=∠ACB=90°,AC与BD交于点O,且AC=BD.有下列结论:①AD=BC;②∠DBC=∠CAD;③AO=BO;④AB∥CD.其中正确的是( )
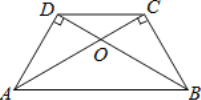
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(3)班共有学生54人,学习委员调查了班级学生参加课外活动的情况(每人只参加一项活动),其中:参加读书活动的18人,参加科技活动的人数占全班总人数的![]() ,参加艺术活动的比参加科技活动的多3人,所调查班级同学参加体育活动情况如图所示,则在扇形图中表示参加体育活动人数的扇形的圆心角大小为( )
,参加艺术活动的比参加科技活动的多3人,所调查班级同学参加体育活动情况如图所示,则在扇形图中表示参加体育活动人数的扇形的圆心角大小为( )
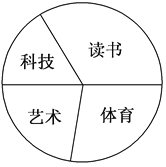
A. 100° B. 110°
C. 120° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是 ![]() ;
;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
A.①②③
B.②③④
C.②③
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA=60°,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s),则点Q的运动速度为 cm/s,使得A、C、P三点构成的三角形与B、P、Q三点构成的三角形全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读)如图1,四边形OABC中,OA=a,OC=3,BC=2,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ [θ,a ]
(理解)若点D与点A重合,则这个操作过程为FZ [45°,3];
(尝试)
(1)若点D恰为AB的中点(如图2),求θ;
(2)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上(如图3),求出a的值;若点E落在四边形OABC的外部,直接写出a的取值范围.
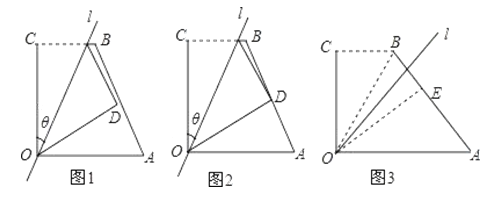
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com