
【题目】如图,已知直线y=ax+b与双曲线y=![]() (x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(1)若A,B两点的坐标分别为(1,3),(3,y2),求点P的坐标;
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
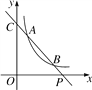
【答案】(1)点P的坐标为(4,0).
(2)点A的坐标为(2,2),点B的坐标为(4,1).
【解析】试题分析:
(1)把A、B的坐标代入![]() 中可求得
中可求得![]() 的值,由此可得B的坐标,再把A、B的坐标代入
的值,由此可得B的坐标,再把A、B的坐标代入![]() 列方程组解得
列方程组解得![]() 的值可得一次函数的解析式,由一次函数的解析式可求得P的坐标;
的值可得一次函数的解析式,由一次函数的解析式可求得P的坐标;
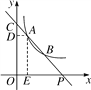
(2)如图,过点A作AD⊥OC于点D,AE⊥OP于点E,由题意知DO=AE=y1,AD=x1,OP=6,OC=b=y1+1,AB=BP,∴CD=OC-OD=y1+1-y1=1,由AD∥x轴,可得![]() ,即
,即![]() ;
;
由AB=BP及线段中点坐标公式可得点B的坐标为(![]() ,
, ![]() y1),再由A、B两点都在反比例函数的图象上可得x1·y1=
y1),再由A、B两点都在反比例函数的图象上可得x1·y1=![]() ·
·![]() y1,解得x1=2,代入
y1,解得x1=2,代入![]() ,解得y1=2,这样就可求得A、B两点的坐标了.
,解得y1=2,这样就可求得A、B两点的坐标了.
试题解析:
(1)∵直线y=ax+b与双曲线y=![]() (x>0)交于A(1,3),∴k=1×3=3,
(x>0)交于A(1,3),∴k=1×3=3,
∴双曲线的解析式为y=![]() .
.
∵B(3,y2)在反比例函数的图象上,
∴y2=![]() =1,
=1,
∴点B的坐标为(3,1).
∵直线y=ax+b经过A,B两点,
∴![]() ,解得
,解得![]()
∴直线的解析式为y=-x+4.令y=0,则x=4,
∴点P的坐标为(4,0).
(2)如图,过点A作AD⊥y轴于点D,AE⊥x轴于点E,则AD∥x轴,
∴![]() .
.
由题意知DO=AE=y1,AD=x1,OP=6,OC=b=y1+1,AB=BP,
∴CD=OC-OD=y1+1-y1=1,
∴![]() .
.
∵AB=BP,
∴由线段中点坐标公式可得点B的坐标为(![]() ,
, ![]() y1).
y1).
∵A,B两点都是反比例函数图象上的点,
∴x1·y1=![]() ·
·![]() y1,解得x1=2,代入
y1,解得x1=2,代入![]() ,解得y1=2,
,解得y1=2,
∴点A的坐标为(2,2),点B的坐标为(4,1).


科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形统计图(如图①)和条形统计图(如图②),经确认扇形统计图是正确的,而条形统计图尚有一处错误.
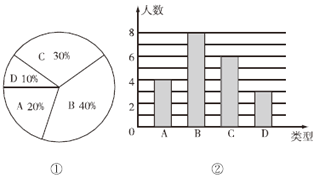
回答下列问题:
(1)写出条形统计图中存在的错误,并说明理由.
(2)写出这20名学生每人植树量的众数、中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<![]() ),连接MN.
),连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
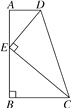
【题目】)如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.
(1)求证:△ADE∽△BEC;
(2)若AD=1,DE=![]() ,BC=2,求AB的长.
,BC=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
(1)求证:△ACD≌△EDC;
(2)若点D是BC中点,说明四边形ADCE是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com