
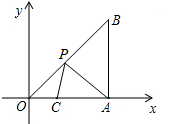
 如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(4,4),点C的坐标为(1,0),点P为斜边OB上的一个动点,当PA+PC的值最小值时,点P的坐标为($\frac{4}{5}$,$\frac{4}{5}$).
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(4,4),点C的坐标为(1,0),点P为斜边OB上的一个动点,当PA+PC的值最小值时,点P的坐标为($\frac{4}{5}$,$\frac{4}{5}$). 分析 作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小根据已知条件得到AB=4,OA=4,△AOB是等腰直角三角形,
推出D在y轴上,过P作PE⊥OA于E,设PE=OE=x,于是得到CE=1-x,根据相似三角形的性质得到$\frac{CE}{OC}=\frac{PE}{OD}$,即$\frac{1-x}{1}=\frac{x}{4}$,求得PE=OE=$\frac{4}{5}$,于是得到结论.
解答 解:作A关于OB的对称点D,连接CD交OB于P,连接AP,
则此时PA+PC的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵B(4,4),
∴AB=4,OA=4,
∵tan∠AOB=$\frac{AB}{OA}$=1,
∴∠AOB=45°,
∴△AOB是等腰直角三角形,
∴OB=$\sqrt{2}$AB=4$\sqrt{2}$,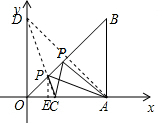
∴AD=2AP=2PD=4$\sqrt{2}$,
∴∠OAP=45°,
∴D在y轴上,
∴OD=OA=4,
过P作PE⊥OA于E,
∴PE=OE,
设PE=OE=x,
∴CE=1-x,
∵PE∥OD,
∴△PCE∽△CDO,
∴$\frac{CE}{OC}=\frac{PE}{OD}$,即$\frac{1-x}{1}=\frac{x}{4}$,
∴x=$\frac{4}{5}$,
∴PE=OE=$\frac{4}{5}$,
∴P($\frac{4}{5}$,$\frac{4}{5}$).
故答案为:($\frac{4}{5}$,$\frac{4}{5}$).
点评 本题考查了轴对称-最短路线问题,勾股定理,三角形相似的判定和性质,关键是求出P点的位置,题目比较好,难度适中.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16条 | B. | 12条 | C. | 8条 | D. | 4条 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象必过点(0,0) | |
| B. | 直线与坐标轴围成的三角形的面积为0.5 | |
| C. | 图象经过第一、二、三象限 | |
| D. | y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}2x+9y=0\\ x+y=0\end{array}\right.$ | B. | 3x=4y=1 | C. | $\left\{\begin{array}{l}\frac{1}{x}-2y=2\\ x=1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a+3b=5ab | B. | -2x2-x2=-3x4 | C. | -1.5-2$\frac{1}{2}$=-4 | D. | -32=(-3)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | (20,0) | B. | (20,1) | C. | (21,0) | D. | (21,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com