
【题目】为疏导国庆假期交通,一辆交通巡逻车在南北公路上巡视.某天早上从![]() 地出发,中午到达
地出发,中午到达![]() 地,行驶记录如下(规定向北为正方向,单位:千米):
地,行驶记录如下(规定向北为正方向,单位:千米):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
请你解答下列问题:
(1)![]() 地在
地在![]() 地的什么方向?与
地的什么方向?与![]() 地相距多远?
地相距多远?
(2)巡逻车在巡逻中,离开![]() 地最远多少千米?
地最远多少千米?
(3)若巡逻车行驶每千米耗油![]() 升,这半天共耗油多少升?
升,这半天共耗油多少升?
科目:初中数学 来源: 题型:
【题目】(1)写出方程 x + y =3的两个解__________,把方程 x + y =3化成一次函数的形式为__________;
(2)以方程 x + y =3的解为坐标的所有点组成的图象与一次函数 y =3- x 的图象相同吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面给出的五个结论中:
①最大的负整数是-1;②数轴上表示数3和-3的点到原点的距离相等;
③当a≤0时,|a|=-a成立;④若a2=9,则a一定等于3;
⑤![]() 一定是正数.说法正确的有_________________
一定是正数.说法正确的有_________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相较于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH. 
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HGHB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用平方根去根号可以构造一个整系数方程.例如:x= ![]() +1时,移项得x﹣1=
+1时,移项得x﹣1= ![]() ,两边平方得(x﹣1)2=(
,两边平方得(x﹣1)2=( ![]() )2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x=
)2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x= ![]() 时,可以构造出一个整系数方程是( )
时,可以构造出一个整系数方程是( )
A.4x2+4x+5=0
B.4x2+4x﹣5=0
C.x2+x+1=0
D.x2+x﹣1=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:
①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;
②三角形的三边a、b、c满足a2+c2=b2,则∠C=90°;
③△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④△ABC中,若 a:b:c=1:2:![]() ,则这个三角形是直角三角形.
,则这个三角形是直角三角形.
其中,正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(1,5)在函数![]() (x>0)的图象上,过点P分别作x轴、y轴的垂线,垂足为点A,B;Q(m,n)为图象上另一动点,过点Q分别作x轴、y轴的垂线,垂足为点C、D.随着m的增大,四边形OCQD四边形OAPB不重叠部分的面积 ( )
(x>0)的图象上,过点P分别作x轴、y轴的垂线,垂足为点A,B;Q(m,n)为图象上另一动点,过点Q分别作x轴、y轴的垂线,垂足为点C、D.随着m的增大,四边形OCQD四边形OAPB不重叠部分的面积 ( )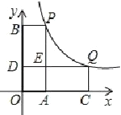
A. 先增大后减小 B. 先减小后增大
C. 先减小后增大再减小 D. 先增大后减小再增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com