
| A. | m>0 | B. | m<0 | C. | m>1 | D. | m<1 |
分析 将一次函数解析式代入反比例函数解析式中整理后即可得出关于x的一元二次方程,由两函数图象有两个交点即可得出关于x的一元二次方程有两个不相等的实数根,根据根的判别式△=4+4km>0结合k<0即可得出m<-$\frac{1}{k}$,对照四个选择即可得出结论.
解答 解:(1)将y1=kx+2代入y2=$\frac{m}{x}$中,整理得:
kx2+2x-m=0.
∵一次函数y1=kx+2(k<0)与反比例函数y2=$\frac{m}{x}$(m≠0)的图象相交于A、B两点,
∴方程kx2+2x-m=0有两个不相等的实数根,
∴△=22-4k•(-m)=4+4km>0,
∵k<0,
∴m<-$\frac{1}{k}$.
对比四个选项即可知B符合题意.
故选B.
点评 本题考查了反比例函数与一次函数的交点问题、根的判别式以及解一元一次不等式,由两函数图象交点的个数结合根的判别式找出关于m的一元一次不等式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,正在播放《中国好声音》 | |
| B. | 上学路上经过十字路口遇上红灯 | |
| C. | 掷一枚均匀的硬币,正面朝上 | |
| D. | 从1、2、3、4、5这五个数中任取一个数,取到的数一定大于0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
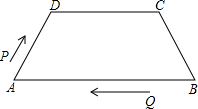 如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为( )
如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为( )| A. | 4s | B. | 3 s | C. | 2 s | D. | 1s |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不等式x+1≤4的整数解有无数个 | B. | 不等式x+4<5的解集是x<1 | ||
| C. | 不等式x<4的正整数解为有限个 | D. | 0是不等式3x<-1的解 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 场次(场) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 得分(分) | 13 | 4 | 13 | 16 | 6 | 19 | 4 | 4 | 7 | 18 |
| A. | 10,4 | B. | 10,13 | C. | 11,4 | D. | 12.5,13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
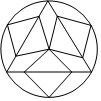 如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )
如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与正方形的边长的比值为( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\frac{{3\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com