练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知∠AOB.求作：∠AOB的平分线.(要求：尺规作图，保留作图痕迹，不必写作法)，这种尺规作图得到角平分线的依据是______.

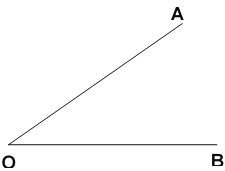
    【答案】作图见解析；三条边对应相等的两个三角形全等，全等三角形对应角相等.

    【解析】

    ①以点O为圆心，以适当长为半径作弧交OA、OB于C、D；②分别以点C、D为圆心，以大于CD长为半径作弧，两弧相交于点E；③作射线OE，OE即是∠AOB的平分线；连结CE，DE，根据SSS可证△OCE≌△ODE，可得∠COE=∠DOE，问题得解.

    解：如图，射线OE即为所求：

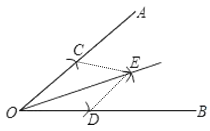
    连结CE，DE，

    由作图可知：OC=OD，CE=DE，

    ∵OE=OE，

    ∴△OCE≌△ODE（SSS），

    ∴∠COE=∠DOE，即OE为∠AOB的平分线，

    ∴这种尺规作图得到角平分线的依据是：三条边对应相等的两个三角形全等，全等三角形对应角相等.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD⊥BC，垂足为D，AD=CD，点E在AD上，DE=BD，M、N分别是AB、CE的中点．

    （1）求证：△ADB≌△CDE；

    （2）求∠MDN的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题提出）

    学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．

    （初步思考）

    我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

    （深入探究）

    第一种情况：当∠B是直角时，△ABC≌△DEF．

    （1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据 ，可以知道Rt△ABC≌Rt△DEF．

    第二种情况：当∠B是钝角时，△ABC≌△DEF．

    （2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．

    第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．

    （3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）

    （4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若 ，则△ABC≌△DEF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四张质地相同的卡片如图所示．将卡片洗匀后,背面朝上放置在桌面上．

    (1)求随机抽取一张卡片,恰好得到数字2的概率;

    (2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图．你认为这个游戏公平吗?请用列表法或画树形图法说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，有点A(2，0)，B(0，3)，C(0，2)，且△AOB与△OCD全等．请直接写出点D的坐标________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：直线l1与直线l2平行，且它们之间的距离为3，A，B是直线l1上的两个定点，C，D是直线l2上的两个动点（点C在点D的左侧），AB=CD=6，连接AC、BD、BC，将△ABC沿BC折叠得到△A1BC．（如图1）

    （1）当A1与D重合时（如图2），四边形ABDC是什么特殊四边形，为什么？

    （2）当A1与D不重合时，连接A1D，则A1 D∥BC（不需证明），此时若以A1，B，C，D为顶点的四边形为矩形，且矩形的边长分别为a，b，求（a+b）2的值．

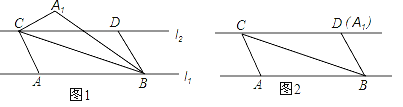
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，AC=6，BD=6，E是BC边的中点，P，M分别是AC，AB上的动点，连接PE，PM，则PE+PM的最小值是（　　）

    A. 6 B. 3 C. 2 D. 4.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了增强学生的环保意识，某校组织了一次全校2000名学生都参加的“环保知识”考试，考题共10题．考试结束后，学校团委随机抽查部分考生的考卷，对考生答题情况进行分析统计，发现所抽查的考卷中答对题量最少为6题，并且绘制了如下两幅不完整的统计图．请根据统计图提供的信息解答以下问题：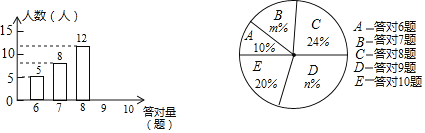

    （1）本次抽查的样本容量是　 　；在扇形统计图中，m=　 　，n=　 　，“答对8题”所对应扇形的圆心角为　 　度；

    （2）将条形统计图补充完整；

    （3）请根据以上调查结果，估算出该校答对不少于8题的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，计划围一个面积为50 m2的长方形场地，一边靠旧墙(墙长为10 m)，另外三边用篱笆围成，并且它的长与宽之比为5∶2.讨论方案时，小英说：“我们不可能围成满足要求的长方形场地．”小军说：“面积和长宽比例是确定的，肯定可以围得出来．”请你判断谁的说法正确，为什么？

    查看答案和解析>>

    同步练习册答案