
����Ŀ����ͼ1����P��Q�ֱ��DZ߳�Ϊ4cm�ĵȱ�������ABC�ı�AB��BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s��

��1������AQ��CP���ڵ�M������P��Q�˶��Ĺ����У�֤��![]() ��
��![]() ��
��
��2��![]() �ᷢ���仯�����仯����˵�����ɣ������䣬��������Ķ�����
�ᷢ���仯�����仯����˵�����ɣ������䣬��������Ķ�����
��3��P��Q�˶�����ʱ��![]() ��ֱ�������Σ�
��ֱ�������Σ�
��4����ͼ2������P��Q���˶����յ�����������AB��BC���˶���ֱ��AQ��CP����ΪM����![]() �仯�����仯˵�����ɣ������䣬��������Ķ�����
�仯�����仯˵�����ɣ������䣬��������Ķ�����
���𰸡���1������������2����CMQ=60�㣬���䣻��3������![]() ����2��ʱ����PBQΪֱ�������Σ���4����CMQ=120�㣬���䣮
����2��ʱ����PBQΪֱ�������Σ���4����CMQ=120�㣬���䣮
��������
��1������SAS��֤ȫ�ȣ�
��2����֤��ABQ�ա�CAP���ó���BAQ=��ACP��ͨ���Ƕ�ת�����ɵó���CMQ=60����
��3������2�������һ���ǡ�PQB=90������һ���ǡ�BPQ=90�����ֱ����ֱ�������α�ֱ�ǵĹ�ϵ�����t��ֵ��
��4����֤��PBC�ա�ACQ���Ӷ��ó���BPC=��MQC��Ȼ�����ýǶ�ת���ɵó���CMQ=120����
��1��֤�����ڵȱ�������ABC�У�AB=AC����B=��CAP=60��
������������P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s.����֪��
AP=BQ
��![]() ��
��![]() ��
��
��2����CMQ=60������
���ȱ��������У�AB=AC����B=��CAP=60��
����������AP=BQ��
���ABQ�ա�CAP(SAS)��
���BAQ=��ACP��
���CMQ=��ACP+��CAM=��BAQ+��CAM=��BAC=60����
��3����ʱ��Ϊt����AP=BQ=t��PB=4-t��
������PQB=90��ʱ��
�ߡ�B=60����
��PB=2BQ����4-t=2t��t=![]() ��
��
������BPQ=90��ʱ��
�ߡ�B=60����
��BQ=2PQ����2t=2��4-t����t=2��
������![]() ����2��ʱ����PBQΪֱ�������Σ�
����2��ʱ����PBQΪֱ�������Σ�
��4����CMQ=120�����䣬
���ڵȱ��������У�AB=AC����B=��CAP=60����
���PBC=��ACQ=120����
����������BP=CQ��
���PBC�ա�ACQ(SAS)��
���BPC=��MQC��
���ߡ�PCB=��MCQ��
���CMQ=��PBC=180��-60��=120����


 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
�����龳
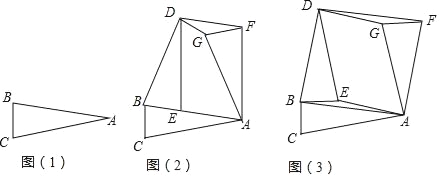
���ۺ�ʵ�����ϣ���ʦ��ͬѧ�ǡ��������ε���ת��Ϊ���������ѧ�����ͼ��1������������ֽƬABC�У�AB=AC����B=��C=����
��������
��1������С�齫ͼ��1���е���ABC�Ե�BΪ��ת���ģ���ʱ����ת�ǶȦ����õ���DBE���ٽ���ABC�Ե�AΪ��ת���ģ�˳ʱ����ת�ǶȦ����õ���AFG������DF���õ�ͼ��2�������ı���AFDE����״���� ����
��2��ʵ��С�齫ͼ��1���е���ABC�Ե�BΪ��ת���ģ���ʱ����ת90�㣬�õ���DBE���ٽ���ABC�Ե�AΪ��ת���ģ�˳ʱ����ת90�㣬�õ���AFG������DF��DG��AE���õ�ͼ��3���������ı���AFDBΪ�����Σ�����֤��������ۣ�
��չ̽��
��3��������ʵ��С������Ļ����ϣ���д��ͼ��3���е�һ�������ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��СҶ��С������������ij����DE�ĸ߶ȣ��������������ǰ����һ��¥ͤǰ��̨���ϵĵ�A��������������D������Ϊ30��������������ķ����ߵ�̨���µĵ�C����������������D������Ϊ60��.��֪��A�ĸ߶�ABΪ3 m��̨��AC���¶�Ϊ1��![]() ����B��C��E������ͬһ��ֱ���ϣ���ô�����DE�ĸ߶�Ϊ(����)
����B��C��E������ͬһ��ֱ���ϣ���ô�����DE�ĸ߶�Ϊ(����)
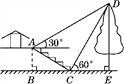
A. 6 m B. 7 m C. 8 m D. 9 m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪˫����y=![]() ��k��0������ֱ��������OABб��OA���е�D������ֱ�DZ�AB�ཻ�ڵ�C������A������Ϊ����6��4��������AOC�����Ϊ��������
��k��0������ֱ��������OABб��OA���е�D������ֱ�DZ�AB�ཻ�ڵ�C������A������Ϊ����6��4��������AOC�����Ϊ��������
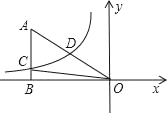
A. 12 B. 9 C. 6 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ž���ֽ�尴ͼ�����߲ü��ɾſ飬�����������DZ߳���Ϊ![]() �Ĵ������Σ������DZ߳���Ϊ
�Ĵ������Σ������DZ߳���Ϊ![]() ��С�����Σ�����dz�Ϊ
��С�����Σ�����dz�Ϊ![]() ����Ϊ
����Ϊ![]() ��ȫ��С���Σ���
��ȫ��С���Σ���![]() >
> ![]() �������ϳ��ȵ�λ��cm��
�������ϳ��ȵ�λ��cm��
��1���۲�ͼ�Σ����Է��ִ���ʽ![]() ������ʽ�ֽ�Ϊ ��
������ʽ�ֽ�Ϊ ��
��2����ÿ��С���ε����Ϊ10![]() ���ĸ������ε������Ϊ58
���ĸ������ε������Ϊ58![]() ������ͼ�����вü��ߣ����߲��֣���֮�ͣ�
������ͼ�����вü��ߣ����߲��֣���֮�ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�п쳵�ɼؿ����ҵأ�һ���������ҵؿ����أ�����ͬʱ�����������˶����쳵���ҵص�·��![]() ����ʻ��ʱ��
����ʻ��ʱ��![]() ֮��ĺ�����ϵ����ͼ���߶�AB��ʾ���������ҵص�·��
֮��ĺ�����ϵ����ͼ���߶�AB��ʾ���������ҵص�·��![]() ����ʻ��ʱ��
����ʻ��ʱ��![]() ֮��ĺ�����ϵ����ͼ���߶�OC��ʾ������ͼ����������о���
֮��ĺ�����ϵ����ͼ���߶�OC��ʾ������ͼ����������о���
![]() �쳵���ٶ���________
�쳵���ٶ���________![]() ���������ٶ���________
���������ٶ���________![]() ��
��
![]() ��AB��OC�ĺ�����ϵʽ��
��AB��OC�ĺ�����ϵʽ��
![]() ��ʱ�쳵���ҵصľ�������������ҵصľ��룿
��ʱ�쳵���ҵصľ�������������ҵصľ��룿

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ֧Ԯ������ijУ���ĻС�����óO���ʽ���A��B�����ͺŵ�ѧϰ��Ʒ��1000������֪B��ѧϰ��Ʒ�ĵ��۱�A��ѧϰ��Ʒ�ĵ��۶�10Ԫ����180Ԫ����B��ѧϰ��Ʒ�ļ�������120Ԫ����A��ѧϰ��Ʒ�ļ�����ͬ��
��1����A��B����ѧϰ��Ʒ�ĵ��۸��Ƕ���Ԫ��
��2������������ѧϰ��Ʒ�ķ��ò�����28000Ԫ��������B��ѧϰ��Ʒ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ��AD��BC���ϵ����ߣ���C��AD�Ĵ��ߣ���AB�ڵ�E����AD�ڵ�O����֤��
��AD��BC���ϵ����ߣ���C��AD�Ĵ��ߣ���AB�ڵ�E����AD�ڵ�O����֤��![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ������
������![]() ����
����![]() ������
������![]() �ϣ������
�ϣ������![]() �غϣ�������
�غϣ�������![]() ������
������![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��
��1����ͼ�٣���![]() ����
����![]() ����
����![]() �Ķ�����
�Ķ�����
��2����ͼ�ڣ���![]() ������
������![]() ������
������![]() ���˶�ʱ��
���˶�ʱ��![]() ��
��![]() ֮����������������ϵ����д����Ľ��ۣ�������֤����
֮����������������ϵ����д����Ľ��ۣ�������֤����
��3�� ��ͼ�ۣ��ڣ�2���������£�����![]() ����
����![]() ������
������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ��
��![]() ��
��![]() ������
������![]() ������
������![]() ���˶�ʱ��
���˶�ʱ��![]() ��
��![]() ֮����������������ϵ����д����Ľ��ۣ�������֤����
֮����������������ϵ����д����Ľ��ۣ�������֤����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com