
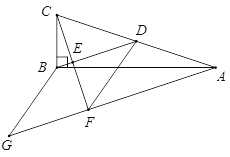
【题目】如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG =BD,连接BG、DF.若AF=8,CF=6,求四边形BDFG的周长.
【答案】四边形BDFG的周长是20.
【解析】试题分析:首先可判断四边形BGFD是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BDFG是菱形,利用勾股定理求得AC的长,即可求得DF的长,即可求得四边形BDFG的周长.
试题解析:∵AG∥BD,BD=FG,∴ 四边形BGFD是平行四边形,
∵ CF⊥BD,∴ CF⊥AG,
又∵ 点D是AC中点, ∴ BD=DF, ∴ 四边形BGFD是菱形,
在Rt△ACF中, AC2 =AF2+CF2即82+62=100,解得:AC=10,
∵ Rt△ACF中,点D是AC中点,∴ DF=5 ,
故四边形BDFG的周长=4GF=20.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】八袋大米,以每袋25千克为标准,称重记录如下(超过标准的千克数记为正数,不足标准的千克数记为负数):+2,-0.5,+3,-1,+2,-1.5,+2.5,+4.这八袋大米总共有多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两人要去某风景区游玩,每天某—时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序,两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车,而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,如果第二辆乍的状况比第一辆好,他就上第二辆车;如果第二辆不比第—辆好,他就上第三辆车.若把这三辆车的舒适程度分为上、中、下三等.请问:
(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年2班组织了一次经典诵读比赛,甲乙两组各10人的比赛成绩如下表(10分制):

(I)甲组数据的中位数是 ,乙组数据的众数是 ;
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是1.4分2,则成绩较为整齐的是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com