
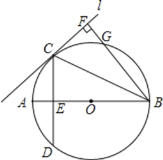
【题目】如图所示,已知AB是![]() 的直径,直线L与
的直径,直线L与![]() 相切于点C,
相切于点C,![]() ,CD交AB于E,
,CD交AB于E,![]() 直线L,垂足为F,BF交
直线L,垂足为F,BF交![]() 于C.
于C.
![]() 图中哪条线段与AE相等?试证明你的结论;
图中哪条线段与AE相等?试证明你的结论;
![]() 若
若![]() ,
,![]() ,求AB的值.
,求AB的值.
【答案】(1)见解析;(2)20.
【解析】
(1)观察图象知:只有FG的长度与AE相当,可猜想AE=FG,然后着手证明它们相等;求简单的线段相等,通常是证线段所在的三角形全等,那么本题需要构造全等三角形,连接AC、CG,然后证△AEC≌△GCF;连接BD,由于弧AC=弧AD,那么BA⊥CD,根据垂径定理知∠D=∠BCE;由弦切角定理知∠FCB=∠D=∠DCB,那么它们的余角也相等,即∠FBC=∠EBC,那么弧CG=弧AC,即AC=CG,再由角平分线的性质得CF=CE,根据HL即可判定所求的两个三角形全等,由此得证.
(2)由弦切角定理知∠FCG=∠FBC,它们的正弦值也相等,即可在Rt△FCG中,求得CG的长,也就得到了AC的长,在Rt△ACB中,CE⊥AB,由射影定理即可得到AB的长.
解:(1)FG=AE,理由如下:
连接CG、AC、BD;
∵![]() ,
,
∴BA⊥CD,
∴![]() ,即∠D=∠BCD;
,即∠D=∠BCD;
∵直线L切⊙O于C,
∴∠BCF=∠D=∠BCD,
∴∠FBC=∠ABC,
∴![]() ,CE=CF;
,CE=CF;
∴AC=CG;
△ACE和△GCF中,AC=CG、CE=CF,∠AEC=∠CFG=90°,
∴Rt△AEC≌Rt△GCF,则AE=FG.
(2)∵FC切⊙O于C,
∴∠FCG=∠FBC,即sin∠FCG=sin∠CBF=![]() ;
;
在Rt△FCG中,FG=AE=4,CG=FG÷sin∠FCG=4![]() ;
;
∴AC=CG=4![]() ;
;
在Rt△ABC中,CE⊥AB,由射影定理得:
AC2=AEAB,即AB=AC2÷AE=20.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段, ![]() ≈1.414,
≈1.414, ![]() ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米). 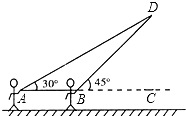
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
点M,N在数轴上分别表示数m和n,我们把m,n之差的绝对值叫做点M,N之间的距离,即MN=|m﹣n|.如图,在数轴上,点A,B,O,C,D的位置如图所示,则DC=|3﹣1|=|2|=2;CO=|1﹣0|=|1|=1;BC=|(﹣2)﹣1|=|﹣3|=3;AB=|(﹣4)﹣(﹣2)|=|﹣2|=2.
![]()
(1)OA= ,BD= ;
(2)|1﹣(﹣4)|表示哪两点的距离?
(3)点P为数轴上一点,其表示的数为x,用含有x的式子表示BP= ,当BP=4时,x= ;当|x﹣3|+|x+2|的值最小时,x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE,过A作AE的垂线交ED于点P,若AE=AP=1,PB=![]() ,下列结论:①△APD≌△AEB;②EB⊥ED;③PD=
,下列结论:①△APD≌△AEB;②EB⊥ED;③PD=![]() ,其中正确结论的序号是( )
,其中正确结论的序号是( )
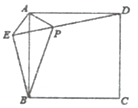
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
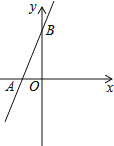
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求直线BP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,在平面直角坐标系中,抛物线y=ax2+3x+c与x轴交于A、B两点,与y轴交于点C(0,8),直线l经过原点O,与抛物线的一个交点为D(6,8).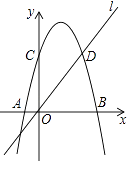
(1)求抛物线的解析式;
(2)抛物线的对称轴与直线l交于点E,点T为x轴上方的抛物线上的一个动点.
①当∠TEC=∠TEO时,求点T的坐标;
②直线BT与y轴交于点P,与直线l交于点Q,当OP=OQ时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l1:y=mx(m≠0) 与直线l2:y=ax+b(a≠0) 相交于点 A(1,2),直线l2与 x轴交于点B(3,0).
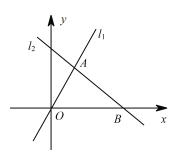
(1)分别求直线l1 和l2的表达式;
(2)过动点P(0,n)且平行于x轴的直线与l1 ,l2的交点分别为C ,D,当点 C 位于点 D 左方时,写出 n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com