
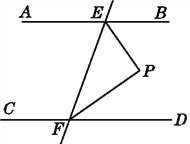
【题目】如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EP平分∠BEF,FP平分∠DFE.试说明:△PEF是直角三角形.
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人 | 甲 | 乙 | 丙 | 丁 | |
测试成绩 (百分制) | 面试 | 86 | 92 | 90 | 83 |
笔试 | 90 | 83 | 83 | 92 | |
如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们![]() 和
和![]() 的权.根据四人各自的平均成绩,公司将录取( )
的权.根据四人各自的平均成绩,公司将录取( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年11月的最后一个星期四是感恩节,小龙调查了初三年级部分同学在感恩节当天将以何种方式表达感谢帮助过自己的人.他将调查结果分为如下四类:A类﹣﹣当面致谢;B类﹣﹣打电话;C类﹣﹣发短信息或微信;D类﹣﹣写书信.他将调查结果绘制成如图不完整的扇形统计图和条形统计图: 请你根据图中提供的信息完成下列各题: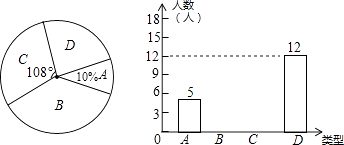
(1)补全条形统计图;
(2)在A类的同学中,有3人来自同一班级,其中有1人学过主持.现准备从他们3人中随机抽出两位同学主持感恩节主题班会课,请你用树状图或表格求出抽出的两人都没有学过主持的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
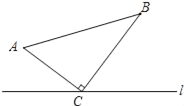
【题目】如图,在△ABC中,∠ACB=90°,AC=5cm,BC=12cm.动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和Q作PE⊥MN于E,QF⊥MN于F.则点P运动时间为_____秒时,△PEC与△QFC全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
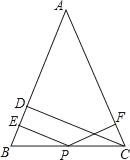
【题目】如图,在△ABC中,AB=AC,CD垂直AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F.
(1)若P为BC边中点,则PE,PF,CD三条线段有何数量关系(写出推理过程)?
(2)若P为线段BC上任意一点,则(1)中关系还成立吗?
(3)若P为直线BC上任意一点,则PE,PF,CD三条线段间有何数量关系(请直接写出).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简
(1)![]() ; (2)(﹣2a2)(3ab2﹣5ab3)
; (2)(﹣2a2)(3ab2﹣5ab3)
(3)(x+3)(x﹣7)﹣x(x﹣1). (4)(a﹣2b+1)(a+2b+1)
(5)(3a﹣b)2﹣(2a+b)2﹣5a(a﹣b) (6)(x+2y)2(x﹣2y)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).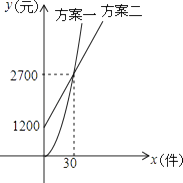
(1)分别求两种方案中y关于x的函数关系式;
(2)当销售达到多少件时,两种方案月报酬差额将达到3800元?
(3)若公司决定改进“方案二”:保持基本工资不变,每件报酬增加m元,使得当销售员销售产量达到40件时,两种方案的报酬差额不超过1000元.求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b满足关系式a=![]() +2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )
+2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )
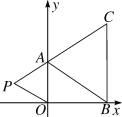
A. (-3,1) B. (-2,1) C. (-4,1) D. (-2.5,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,沿A→B→C路线运动到点C停止;动点Q从点O出发,沿O→E→D→C路线运动到点C停止;若P、Q两点同时出发,且点P的运动速度为1cm/s,点Q的运动速度为2cm/s.
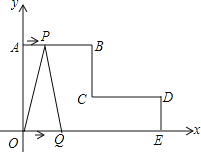
(1)直接写出B、C、D三个点的坐标;
(2)当P、Q两点出发![]() s时,试求△PQC的面积;
s时,试求△PQC的面积;
(3)设两点运动的时间为t s,用t的式子表示运动过程中△OPQ的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com