
【题目】如图1,在直角坐标系中,O是坐标原点,点A在y轴正半轴上,二次函数y=ax2+ ![]() x+c的图象F交x轴于B、C两点,交y轴于M点,其中B(﹣3,0),M(0,﹣1).已知AM=BC.
x+c的图象F交x轴于B、C两点,交y轴于M点,其中B(﹣3,0),M(0,﹣1).已知AM=BC.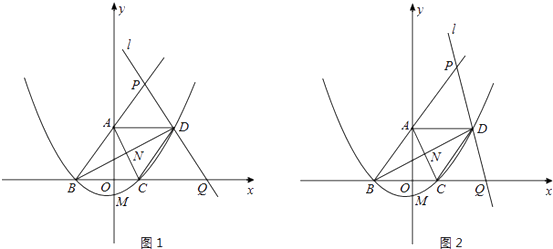
(1)求二次函数的解析式;
(2)证明:在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形,并请求出直线BD的解析式;
(3)在(2)的条件下,设直线l过D且分别交直线BA、BC于不同的P、Q两点,AC、BD相交于N.
①若直线l⊥BD,如图1,试求 ![]() 的值;
的值;
②若l为满足条件的任意直线.如图2.①中的结论还成立吗?若成立,证明你的猜想;若不成立,请举出反例.
【答案】
(1)
解:∵二次函数y=ax2+ ![]() x+c的图象经过点B(﹣3,0),M(0,﹣1),
x+c的图象经过点B(﹣3,0),M(0,﹣1),
∴ 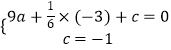 ,
,
解得a= ![]() ,c=﹣1.
,c=﹣1.
∴二次函数的解析式为:y= ![]() x2+
x2+ ![]() x﹣1
x﹣1
(2)
解:由二次函数的解析式为:y= ![]() x2+
x2+ ![]() x﹣1,
x﹣1,
令y=0,得 ![]() x2+
x2+ ![]() x﹣1=0,
x﹣1=0,
解得x1=﹣3,x2=2,∴C(2,0),∴BC=5;
令x=0,得y=﹣1,∴M(0,﹣1),OM=1.
又AM=BC,∴OA=AM﹣OM=4,∴A(0,4).
设AD∥x轴,交抛物线于点D,如图1所示,
则yD= ![]() x2+
x2+ ![]() x﹣1=OA=4,
x﹣1=OA=4,
解得x1=5,x2=﹣6(位于第二象限,舍去)
∴D点坐标为(5,4).
∴AD=BC=5,
又∵AD∥BC,
∴四边形ABCD为平行四边形.
即在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形.
设直线BD解析式为:y=kx+b,∵B(﹣3,0),D(5,4),
∴ ![]() ,
,
解得:k= ![]() ,b=
,b= ![]() ,
,
∴直线BD解析式为:y= ![]() x+
x+ ![]()
(3)
解:在Rt△AOB中,AB= ![]() =5,又AD=BC=5,∴ABCD是菱形.
=5,又AD=BC=5,∴ABCD是菱形.
①若直线l⊥BD,如图1所示.
∵四边形ABCD是菱形,
∴AC⊥BD,
∴AC∥直线l,
∴ ![]() ,
,
∵BA=BC=5,
∴BP=BQ=10,
∴ ![]() =
= ![]() =
= ![]() ;
;
②若l为满足条件的任意直线,如图2所示,此时①中的结论依然成立,理由如下:
∵AD∥BC,CD∥AB,
∴△PAD∽△DCQ,
∴ ![]() ,∴APCQ=ADCD=5×5=25.
,∴APCQ=ADCD=5×5=25.
∴ ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]() .
.
【解析】(1)利用待定系数法求出二次函数的解析式;(2)首先求出D点的坐标,可得AD=BC且AD∥BC,所以四边形ABCD是平行四边形;再根据B、D点的坐标,利用待定系数法求出直线BD的解析式;(3)本问的关键是判定平行四边形ABCD是菱形.①推出AC∥直线l,从而根据平行线间的比例线段关系,求出BP、CQ的长度,计算出 ![]() =
= ![]() ;②判定△PAD∽△DCQ,得到APCQ=25,利用这个关系式对
;②判定△PAD∽△DCQ,得到APCQ=25,利用这个关系式对 ![]() 进行分式的化简求值,结论为
进行分式的化简求值,结论为 ![]() =
= ![]() 不变.
不变.
【考点精析】通过灵活运用平行四边形的判定与性质,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积即可以解答此题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
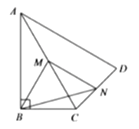
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小杰到学校食堂买饭,看到A、B两窗口前面排队的人一样多(设为a人,a>8),就站在A窗口队伍的后面,过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人.
(1)此时,若小杰继续在A窗口排队,则他到达窗口所花的时间是多少?(用含a的代数式表示)
(2)此时,若小杰迅速从A窗口队伍转移到B窗口后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围.(不考虑其它因素)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场的一个家电商场为了响应国家家电下乡的号召,准备用不超过105700元购进40台电脑,其中A型电脑每台进价2500元,B型电脑每台进价2800元,A型每台售价3000元,B型每台售价3200元,预计销售额不低于123200元.设A型电脑购进x台、商场的总利润为y(元).
(1)请你设计出进货方案;
(2)求出总利润y(元)与购进A型电脑x(台)的函数关系式,并利用关系式说明哪种方案的利润最大,最大利润是多少元?
(3)商场准备拿出(2)中的最大利润的一部分再次购进A型和B型电脑至少各两台,另一部分为地震灾区购买单价为500元的帐篷若干顶.在钱用尽三样都购买的前提下请直接写出购买A型电脑、B型电脑和帐篷的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将点A先向下平移3个单位,再向右平移2个单位后得B(﹣2,5),则A点坐标为( )
A.(﹣4,11)B.(﹣2,6)C.(﹣4,8)D.(﹣6,8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC.中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1 , A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④A1F=CE.其中正确的是(写出正确结论的序号). 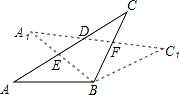
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com