
分析 因为要使圆与斜边只有一个公共点,所以该圆和斜边相切或和斜边相交,但只有一个交点在斜边上.
若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
解答 解:根据勾股定理求得直角三角形的斜边AB=$\sqrt{{8}^{2}+{6}^{2}}$=10,
当圆和斜边相切时,则半径即是斜边上的高,等于$\frac{24}{5}$;
当圆和斜边相交,且只有一个交点在斜边上时,可以让圆的半径大于短直角边而小于长直角边,则6<r≤8.
故半径r的取值范围是r=4.8或6<r≤8.
故答案为:r=4.8或6<r≤8.
点评 此题考查了直线与圆的位置关系,此题注意考虑两种情况,只需保证圆和斜边只有一个公共点即可.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
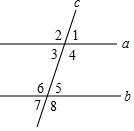 如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )
如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com