
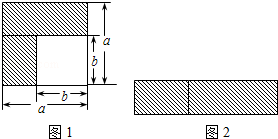
分析 (1)利用大正方形的面积减去小正方形的面积即可;
(2)根据图示可直接得到答案;
(3)把两面积利用等号联立即可;
(4)利用平方差进行计算即可.
解答 解:(1)阴影部分的面积是:a2-b2,
故答案为:a2-b2;
(2)宽是a-b,长是a+b,面积为(a-b)(a+b),
故答案为:a-b;a+b;(a-b)(a+b);
(3)由题意得:(a-b)(a+b)=a2-b2,
故答案为:(a-b)(a+b)=a2-b2;
(4)①$10\frac{1}{3}×9\frac{2}{3}$=(10+$\frac{1}{3}$)(10-$\frac{1}{3}$)=100-$\frac{1}{9}$=99$\frac{8}{9}$;
②(2x-y+3)(2x-3+y),
=[2x-(y-3)][2x+(y-3)],
=(2x)2-(y-3)2,
=4x2-(y2-6y+9),
=4x2-9+6y-y2.
点评 此题主要考查了平方差公式,运用几何直观理解、解决平方差公式的推导过程,通过几何图形之间的数量关系对平方差公式做出几何解释.


科目:初中数学 来源: 题型:解答题
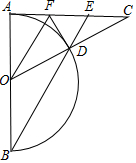 如图,AB为⊙O的直径,AC为⊙O的切线,连接OC,交⊙O于点D,连接BD并延长,交AC于点E,过点O作OF∥BE,交AC于点F,连接DF.
如图,AB为⊙O的直径,AC为⊙O的切线,连接OC,交⊙O于点D,连接BD并延长,交AC于点E,过点O作OF∥BE,交AC于点F,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
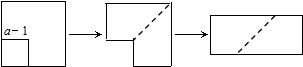
| A. | 1 | B. | a | C. | 2a-1 | D. | 2a+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com