
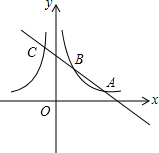
 函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)的图象关于y轴对称,我们定义函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)相互为“影像”函数
函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)的图象关于y轴对称,我们定义函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)相互为“影像”函数分析 (1)关于y轴对称x用-x代替即可.
(2)关于y轴对称x用-x代替即可.
(3)作CC⊥x轴,BB′⊥x轴,AA′⊥x轴垂足分别为C′、B′、A′.设点B(m,$\frac{2}{m}$),A(n,$\frac{2}{n}$),其中m>0,n>0,列出方程组消去n即可解决问题.
解答 解:(1)令-x=x得y=-2x-3,
故答案为y=-2x-3.
(2)令-x=x得y=x2+3x-5,
故答案为y=x2+3x-5.
(3)如图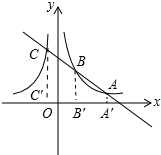 作CC⊥x轴,BB′⊥x轴,AA′⊥x轴垂足分别为C′、B′、A′.
作CC⊥x轴,BB′⊥x轴,AA′⊥x轴垂足分别为C′、B′、A′.
设点B(m,$\frac{2}{m}$),A(n,$\frac{2}{n}$),其中m>0,n>0,
由题意,将x=-1代入y=-$\frac{2}{x}$中解得y=2,
∴点C(-1,2),∴CC′=2,BB′=$\frac{2}{m}$,AA′=$\frac{2}{n}$,
又,A′B′=n-m,B′C′=m+1,CC′∥BB′∥AA′,CB:AB=1:2,
则$\left\{\begin{array}{l}{n-m=2(m+1)}\\{\frac{2}{m}-\frac{2}{n}=\frac{2}{3}(2-\frac{2}{n})}\end{array}\right.$消去n化简得到3m2-2m-3=0,
解得m=$\frac{1+\sqrt{10}}{3}$或$\frac{1-\sqrt{10}}{3}$(舍弃),
∴$\frac{2}{m}$=$\frac{2}{\frac{1+\sqrt{10}}{3}}$=$\frac{-2+2\sqrt{10}}{3}$,
∴点B坐标为($\frac{1+\sqrt{10}}{3}$,$\frac{-2+2\sqrt{10}}{3}$).
点评 本题考查反比例函数的性质、一次函数的性质、平行线的性质等知识,解题的关键是设两个参数m、n,把问题转化为方程组解决,题目有一定难度,属于中考压轴题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:选择题
| A. | .2 | B. | .3 | C. | .4 | D. | .5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线C:y=mx2+4x+1.
在平面直角坐标系xOy中,抛物线C:y=mx2+4x+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
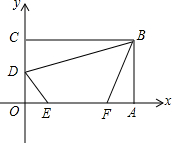 在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )
在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )| A. | ($\frac{1}{2}$,0) | B. | ($\frac{4}{3}$,0) | C. | ($\frac{3}{2}$,0) | D. | (2,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com