如图所示，⊙I是Rt△ABC的内切圆，且分别与BC、AC、AB相切于点D、E、F．

(1)求证：四边形IDCE是正方形；

(2)设BC=a，AC＝b，AC=c，求内切圆的半径r．

答案：
解析：

(1)根据切线的性质和正方形定义证;(2)分别连结IA、IB、IC、IF，有S_△ABC＝

S_△IBC＋S_△IAC＋S_△IAB，可化得r＝进而还可化得r＝(a＋b－c)

练习册系列答案

名校课堂系列答案

相关习题

科目：初中数学 来源： 题型：

如图所示，CD是Rt△ABC斜边AB上的高，AF为角平分线，AF交BC于F，交CD于E，过E作EG∥AB，与BC交于G，过F向AB作垂线，垂足为H．
求证：（1）CF=BG；
（2）四边形CEHF是菱形．

科目：初中数学 来源： 题型：

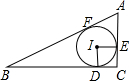如图所示，⊙I是Rt△ABC（∠C=90°）的内切圆，⊙I和三边分别切于点D，E，F．
（1）求证：四边形IDCE是正方形；
（2）设BC=a，AC=b，AB=C，求内切圆I的半径．

科目：初中数学 来源：新课标读想练同步测试　八年级数学(下) 题型：022

如图所示，CD是Rt△ABC斜边AB上的高，那么图中共有________个三角形与△ABC是形状相同的图形．

科目：初中数学 来源： 题型：解答题

如图所示，CD是Rt△ABC斜边AB上的高，AF为角平分线，AF交BC于F，交CD于E，过E作EG∥AB，与BC交于G，过F向AB作垂线，垂足为H．
求证：（1）CF=BG；
（2）四边形CEHF是菱形．

科目：初中数学 来源：《第1章图形与证明（二）》2009年综合水平测试卷（A卷）（解析版） 题型：解答题

同步练习册答案

如图所示，CD是Rt△ABC斜边AB上的高，AF为角平分线，AF交BC于F，交CD于E，过E作EG∥AB，与BC交于G，过F向AB作垂线，垂足为H．求证：（1）CF=BG；（2）四边形CEHF是菱形．