
| 售价x (元) | … | 60 | 65 | 70 | 75 | 80 |
| 月销量y (万箱) | … | 6 | 5.5 | 5 | 4.5 | 4 |
分析 (1)由于图中数据为均匀变化,故可猜想y与x为一次函数关系,设出解析式,利用待定系数法即可求解;
(2)先利用销量乘以每件的销售利润减去月总开支就是每月的销售利润,然后化为顶点式就可以求出月销售的最大利润;
(3)由(2)可以得出最高售价是80元,最大利润是78万元,可以得出2月份的销售数量为4万箱、总开支为82万元.再通过数量关系表示出3月的成本价为40×(1+25%)元,售价为80(1-25%)元,销量为4(1+40%)万箱,就可以求出3月的利润,再通过3月销售情况及数量关系求出4月、5月的销售利润建立等量关系,就可以n的值.
解答 解:(1)设解析式为y=kx+b,
将(60,6),(70,5)分别代入解析式得,
$\left\{\begin{array}{l}{6=60k+b}\\{5=70k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{10}}\\{b=12}\end{array}\right.$,
则解析式为y=-$\frac{1}{10}$x+12;
(2)设月销售利润为W,由题意,得
W=(x-40)(-0.1x+12)-(10y+42)
=-0.1x2+12x+4x-480-10(-0.1x+12)-42
=-0.1(x-85)2+80.5,
∵a=-0.1<0,
∴抛物线的开口向下,在抛物线的左侧W随x的增大而增大,
∴当x=85时,W有最大值80.5.
∵x为5的倍数,且x≤80元,
∴x=80时,W有最大值:78;
(3)由题意,得
二月的销量为:-$\frac{1}{10}$×80+12=4,
二月的总开支为:10×4+42=82万元,
∴3月的成本价为40×(1+25%)=50元,
售价为80(1-25%)=60元.
销量为4(1+40%)=5.6万箱.
∴3月的利润为:5.6(60-50)-82-5-250=-281万元.
∴4月份售价为60(1+n%),销量为:5.6(1+0.25n%),
∴4月的利润为:[60(1+n%)-50][5.6(1+0.25n%)]-87,
∴{[60(1+n%)-50][5.6(1+0.25n%)]-87}×2+78-281=295,
设n%=m,则{[60(1+m)-50][5.6(1+0.25m)]-87}×2+78-281=295,
化简为:6m2+25m-20=0
解得m=$\frac{-25±\sqrt{1105}}{12}$,
m1=$\frac{-58}{12}$(不符合题意,应舍去).
m2=$\frac{8}{12}$=66.7%.
∴n=67.
点评 本题考查了待定系数法求一次函数的解析式,二次函数的解析式及顶点式求函数的最值.在解答时要注意未知数的值要使实际问题有意义.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
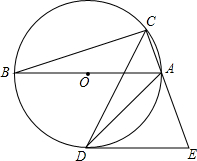 如图,⊙O是△ABC的外接圆,AB为⊙O的直径,∠ACB的平分线交⊙O于点D,点E在CA的延长线上,且DE为⊙O切线.
如图,⊙O是△ABC的外接圆,AB为⊙O的直径,∠ACB的平分线交⊙O于点D,点E在CA的延长线上,且DE为⊙O切线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com