
����Ŀ��(12��)��ͼ1����֪Rt��ABC����AB��BC��AC��2����һ�麬30���ǵ����ǰ�DEF��ֱ�Ƕ���D����AC���е���(ֱ�����ǰ�Ķ�ֱ�DZ�ΪDE����ֱ�DZ�ΪDF)����C��DE������B��DF�ϣ�
(1)���ص�������BCD�������
(2)��ͼ2����ֱ�����ǰ�DEF��D�㰴˳ʱ�뷽����ת30����DE��BC�ڵ�M��DF��AB�ڵ�N.
����֤��DM��DN��
���ڴ��������ص����ֵ�����ᷢ���仯���������仯��������ص����ֵ���������������仯����˵�����ɣ�
(3)��ͼ3����ֱ�����ǰ�DEF��D�㰴˳ʱ�뷽����ת����(0������90)��DE��BC�ڵ�M��DF��AB�ڵ�N����DM��DN�Ľ����Գ������ص����ֵ���������(��ֱ��д������������Ҫ˵������)

���𰸡�(1) ![]() (2)�ټ����� �ڲ��� (3) �Գ���������
(2)�ټ����� �ڲ��� (3) �Գ���������
���������������:(1)�ص�������BCD��һ������ֱ��������,�����ֱ�DZ�,�������,
(2)����BD,���ݵ���ֱ�������ε����ʿɵ�: ��C=��ABD=45��,CD=BD,
����Ϊ��CDM+��BD M=��BDN+��BDM=90��,���ԡ�CDM =��BDN,
���ݽDZ߽ǿ����ж���CDM�ա�BDN,�����ص������ı��ε����������BCD�����,���������,
(3)����BD,����(2)�еĽ���˼·��֤��CDM�ա�BDN,�����ص������ı��ε����������BCD�����,���������.
�������: (1)��AB=BC,AC=2,D��AC���е�,
��CD=BD=![]() AC=1,BD��AC.
AC=1,BD��AC.
��S��BCD��![]() CD��BD=
CD��BD=![]() ��1��1=
��1��1=![]() .
.
(2)��֤��:����BD,��BD��ֱƽ��AC.
��BD=CD,��C=��NBD=45��,
�֡ߡ�CDM=��BDN,
���CDM�ա�BDN(ASA)��
��DM=DN.
���ɢ�֪��CDM�ա�BDN����S�ı���BNDM��S��BCD��![]() �������������ص����ֵ�������䣬Ϊ
�������������ص����ֵ�������䣬Ϊ![]() .
.
(3)DM=DN�Ľ����Գ���,�ص����ֵ���������.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ѧ���ϣ�С��ͬѧ��С��ͬѧ����һ�����ν�ϵ��ۺ��⣬�����������ģ���ͼ���������������� M��N ��ʼʱ����ʾ�����ֱ�Ϊ��10��5��M��N ���������һ�����ٶ����������˶����� M ����˶��ٶ�Ϊ2����λ����/s��
��1��M��N ����ͬʱ����������У���ԭ�㴦�������� N ����˶��ٶ���
��2��M��N ���㰴����ĸ����ٶ�ͬʱ�������������������˶�������ʱ�������6����λ���ȣ�
��3��M��N ���㰴����ĸ����ٶ�ͬʱ�����������Ḻ�����˶������ͬʱ��C ���ԭ�������ͬ�����˶��������˶������У�ʼ���� CN��CM=1��2���������C ������12 �������ʱ N ���������ϵ�λ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,�����ɸ�������ֱ�Ϊ�����ĵ�,��˳��ͼ����������������,��(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),��.�����������,��2 025���������Ϊ________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����֯��һ�ζ�����ͳ����16��ͬѧ��һ���ڵĶ���ʱ�䣬����һ���ڵĶ���ʱ���ۼ����������16��ͬѧһ�����ۼƶ���ʱ�����λ���� ��
һ�����ۼƵĶ���ʱ�䣨Сʱ�� | 5 | 8 | 10 | 14 |
���������� | 1 | 7 | 5 | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2+ax+a��2=0��
��1�����÷��̵�һ����Ϊ2����a��ֵ���÷��̵���һ����
��2����֤������aȡ��ʵ�����÷��̶�����������ȵ�ʵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��B��F��C�ĵ���һ��ֱ���ϣ�EB=CF ����A =��D����������һ�������Բ���֤����ABC �ա�DEF���ǣ� ��

A. ��DEF=��ABC B. DF��AC C. AB��DE D. AB =DE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϵ�һ������̨����һ������AB��һ���ܰ�AC�ͻ��ۣ����ƿ��ȣ���Ϊ��A����ɣ������ʾ��ͼΪ��ABC�����AC��BC��AB=5cm��AC=4cm����Ϊ����д���·��㣬�����̨���İڷţ��ƶ���C��C�䣬����C��=30��ʱ�����ƶ��ľ��뼴CC��ij������ü��������㣬���ȡ���������� ![]() =1.732��
=1.732�� ![]() =4.583��
=4.583�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=x2+2x��3���Ѵ���������y������ƽ�ƣ�ƽ�ƺ�������ߺ�ԭ�������뾭���㣨��2��0������2��0����ƽ����y�������ֱ����Χ�ɵ���Ӱ���ֵ����Ϊs��ƽ�Ƶľ���Ϊm��������ͼ���У��ܱ�ʾs��m�ĺ�����ϵ��ͼ������ǣ� ��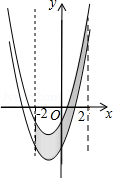
A.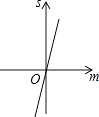
B.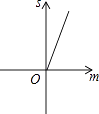
C.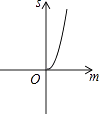
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������Ľ����������ߺͳ����ι��ɣ������εij���12m������4m������ͼ����ʾ��ֱ������ϵ�������߿�����y=�� ![]() x2+bx+c��ʾ���������ߵĵ�C��ǽ��OB��ˮƽ����Ϊ3mʱ��������OA�ľ���Ϊ
x2+bx+c��ʾ���������ߵĵ�C��ǽ��OB��ˮƽ����Ϊ3mʱ��������OA�ľ���Ϊ ![]() m��
m�� 
��1����������ߵĺ�����ϵʽ�������������D������OA�ľ��룻
��2��һ������������һ�����弯װ����Ϊ6m����Ϊ4m�������������˫���г�������ô���������ܷ�ȫͨ����
��3������������������Ҫ��װ���ŵƣ�ʹ���������ĸ߶���ȣ�����������ĸ߶Ȳ�����8m����ô���ŵƵ�ˮƽ������С�Ƕ����ף�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com