练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
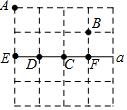
    6．如图的4×4的正方形网格中，有A、B两点，在直线a上求一点P，使PA+PB最短，则点P应选在（　　）
    A．C点B．D点C．E点D．F点

    分析 首先求得点A关于直线a的对称点A′，连接A′B，即可求得答案．

    解答 解：如图，点A′是点A关于直线a的对称点，连接A′B，则A′B与直线a的交点，即为点P，此时PA+PB最短，
    ∵A′B与直线a交于点C，
    ∴点P应选C点．
    故选A．

    点评 此题考查了最短路径问题．注意首先作出其中一点关于直线L的对称点，对称点与另一点的连线与直线L的交点就是所要找的点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．先化简，再求值：$\frac{2x}{x+1}$-$\frac{2x+4}{{x}^{2}-1}$÷$\frac{x+2}{{x}^{2}-2x+1}$，其中x=8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

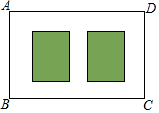    17．要对一块长90米，宽40米的矩形荒地ABCD进行绿化和硬化，设计方案如图所示，矩形P，Q为两块绿地，其余为硬化路面，P、Q两块绿地周围的硬化路面宽度都相等，并使两块绿地面积的和为矩形ABCD面积的$\frac{1}{3}$，求P、Q两块绿地周围的硬化路面的宽．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．下列运算正确的是（　　）
    A．a-（b-c）=a-b-cB．a-（b-c）=a+b+cC．a-（b-c）=a-b+cD．a-（b-c）=a+b-c

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．化简
    （1）$\sqrt{8}$+$\sqrt{18}$；
    （2）（$\sqrt{6}$-2$\sqrt{3}$）×$\sqrt{3}$-6$\sqrt{\frac{1}{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．（1）求x的值：（2x）2=0.25；
    （2）计算：$\sqrt{（-6）^{2}}$-$\root{3}{-8}$+（-$\sqrt{5}$）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．一条关于数学学习方法的微博在一周内转发了318000次，将318000用科学记数法可以表示为（　　）
    A．3.18×105B．31.8×105C．318×104D．3.18×104

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

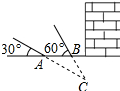    15．如图，某武警部队在一次地震抢险救灾行动中，探险队员在相距4米的水平地面A，B两处均探测出建筑物下方C处有生命迹象，已知在A处测得探测线与地面的夹角为30°，在B处测得探测线与地面的夹角为60°，求该生命迹象C处与地面的距离．（结果精确到0.1米，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）计算：$\sqrt{8}$-（-2016）0+|-3|-4cos45°
    （2）化简求值：（$\frac{a}{a+2}$+$\frac{1}{{a}^{2}-4}$）÷$\frac{a-1}{a+2}$+$\frac{1}{a-2}$，其中a=2+$\sqrt{2}$．

    查看答案和解析>>

    同步练习册答案