
【题目】如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层… 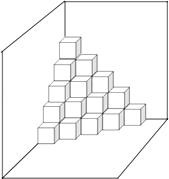
(1)第三层有个小正方体.
(2)从第四层至第六层(含第四层和第六层)共有个小正方体.
(3)第n层有个小正方体.
(4)若每个小正方体边长为a分米,共摆放了n层,则要将摆放的小正方体能看到的表面部分涂上防锈漆,则防锈漆的总面积为分米2 .
【答案】
(1)6
(2)46
(3)![]()
(4)![]() n(n+1)
n(n+1)
【解析】解:(1)第1层,共1个小正方体,
第2层正方体的个数为1+2=3,
第3层正方体的个数为:1+2+3=6.
所以答案是:6.(2)第4层正方体的个数为:10,
第5层正方体的个数为:15,
第6层正方体的个数为:21,
所以从第三层至第六层(含第三层和第六层)共有:10+15+21=46.
所以答案是:46.(3)根据(1)相应规律,可得第n层正方体的个数为1+2+3+…+n= ![]() ;(4)共摆放n层,则靠墙小正方形的面的个数:2×(1+2+3+…+n)=n(n+1),
;(4)共摆放n层,则靠墙小正方形的面的个数:2×(1+2+3+…+n)=n(n+1),
地面接触小正方形的面的个数:1+2+3+…+n= ![]() ,
,
所以靠墙及地面的部分涂上防锈漆的面积为:[n(n+1)+ ![]() ]×a2=
]×a2= ![]() n(n+1)分米2 .
n(n+1)分米2 .
所以答案是:(1)6;(2)41;(3) ![]() ;(4)
;(4) ![]() n(n+1).
n(n+1).


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程( )
A.0.8x﹣10=90
B.0.08x﹣10=90
C.90﹣0.8x=10
D.x﹣0.8x﹣10=90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论: ①AE=CF;
②△EPF是等腰直角三角形;
③S四边形AEPF= ![]() S△ABC;
S△ABC;
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合) BE+CF=EF.
上述结论中始终正确的有( )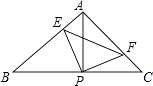
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践探究,解决问题
如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ACD . 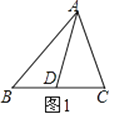
(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,则S阴影=;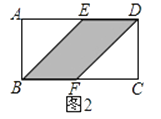
(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴影和S平行四边形ABCD之间满足的关系式为;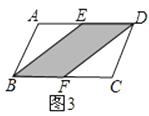
(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴影和S四边形ABCD之间还满足(2)中的关系式吗?若满足,请予以证明,若不满足,说明理由.
解决问题: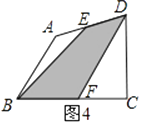
(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和(即S1+S2+S3+S4的值).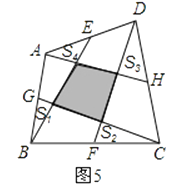
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为鼓励市民节约使用燃气,对燃气进行分段收费,每月使用11立方米以内(包括11立方米)每立方米收费2元,超过部分按每立方米2.4元收取.如果某户使用9立方米燃气,需要燃气费为_____元;如果某户的燃气使用量是x立方米(x超过11),那么燃气费用y与x的函数关系式是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知M,N表示单项式,且3x(M-5x)=6x2y3+N,则( )
A. M=2xy3,N=-15x B. M=3xy3,N=-15x2
C. M=2xy3,N=-15x2 D. M=2xy3,N=15x2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合, OD与BC交于点E,设点D的坐标是![]() ,则
,则![]() 的值为( )
的值为( )
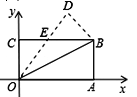
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com