
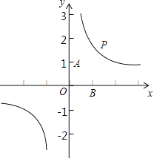
����Ŀ����ͼ����P�Ǻ���y![]() �ϵ�һ������һ�����㣬��A������Ϊ��0��1������B������Ϊ��1��0����
�ϵ�һ������һ�����㣬��A������Ϊ��0��1������B������Ϊ��1��0����
��1������PA��PB��AB������PAB�����ΪS����P�ĺ�����Ϊt����д��S����t�ĺ�����ϵʽ����ָ���Ա���t��ȡֵ��Χ��
��2���Ķ�����IJ��ϻش�����
�Ķ����ϣ� ��a>0ʱ��![]()
��Ϊ![]() ��
��![]() ����a=1ʱ��
����a=1ʱ��![]()
����a=1ʱ��![]() ����СֵΪ2.
����СֵΪ2.
�������������ڣ�1�����о���tΪ��ֵʱ��PAB�����S����Сֵ�������S����Сֵ��
���𰸡���1��S��![]() ��t��0���� ��2����t
��t��0���� ��2����t![]() ʱ��S����СֵΪ
ʱ��S����СֵΪ![]() ��
��
��������
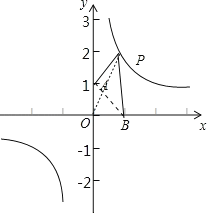
��1������OP��AB�����ݷ���������ͼ���ϵ��������������P������Ϊ��t��![]() �������������������ʽ��S=S��PAO+S��POB��S��OAB��⣻
�������������������ʽ��S=S��PAO+S��POB��S��OAB��⣻
��2������S�T![]() �������Ķ����ϵõ���t��0ʱ��
�������Ķ����ϵõ���t��0ʱ��![]() ��
��![]() ��2
��2![]() �����÷Ǹ��������ʵõ�t
�����÷Ǹ��������ʵõ�t![]() ʱ��
ʱ��![]() ����СֵΪ
����СֵΪ![]() ������t
������t![]() ʱ��S����СֵΪ
ʱ��S����СֵΪ![]() ��
��
��1������OP��AB����ͼ����P������Ϊ��t��![]() ����S=S��PAO+S��POB��S��OAB
����S=S��PAO+S��POB��S��OAB
![]() 1��t
1��t![]() 1
1![]() 1��1
1��1![]()
![]() ��t��0����
��t��0����
��2����t��0ʱ��![]() ��
��![]() ��2
��2![]() ��
��![]() ��2
��2![]() ��
��![]() ��2
��2![]() ������
������![]() ��2��0����
��2��0����![]() ����t
����t![]() ʱ����
ʱ����![]() ��2=0�����Ե�t
��2=0�����Ե�t![]() ʱ��
ʱ��![]() ����СֵΪ
����СֵΪ![]() ������t
������t![]() ʱ��S����СֵΪ
ʱ��S����СֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̶�м�2017��ɹ�����ȫ����������֮����������ȫ���������У�ijС��������Ӧ��������С���ڰ�װ�����������ܰ��ʾ�ƺ������䣬������2����ܰ��ʾ�ƺ�3�������乲��550Ԫ����������ĵ�������ܰ��ʾ�Ƶ��۵�3����
��1������ܰ��ʾ�ƺ�������ĵ��۸��Ƕ���Ԫ��
��2����С��������Ҫ����48�������䣬���������ܰ��ʾ�ƺ������乲100�����ҷ��ò�����10000Ԫ�������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�п쳵�Ӽ�����ʻ���ҵ�,һ���������ҵ�����ʻ����.���ȷ�������ʻ��ʱ��ΪxСʱ,����֮��ľ���Ϊyǧ��,ͼ�е����߱�ʾy��x֮��ĺ�����ϵ.������֮��ľ����״�Ϊ300ǧ��ʱ,����_____Сʱ��,����֮��ľ����ٴ�Ϊ300ǧ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����Rt��ABC��б��BCΪһ������ABC��ͬ����������BCEF���������ε�����ΪO������AO�����AB=4��AO=6![]() ����ôAC=_____��
����ôAC=_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ȼ���������ǵ�������ɾ��Ļ�ʯ��Դ�����㷺���������������У�2019��1��1����ij��Ȼ������˾�Ծ�����������Ȼ�����е������±�Ϊ2018�ꡢ2019������Ľ��ݼ۸�
���� | �û��������� ����λ�������ף� | 2018�굥�� ����λ��Ԫ/�����ף� | 2019�굥�� ����λ��Ԫ/�����ף� |
��һ���� | 0-300������ |
| 3 |
�ڶ����� | 300-600������ |
| 3.5 |
�������� | 600���� |
| 5 |
��1�����û���2018����������Ϊ280�����ף����ܷ���Ϊ Ԫ���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2�����û���2018����������Ϊ450�����ף��ܷ���Ϊ1200Ԫ����![]() ��ֵ��
��ֵ��
��3���ڣ�2���������£����û���2018���2019�깲����Ȼ��1200�����ף�2018������������2019�����������ܷ���Ϊ3625Ԫ������û�2018���2019��ֱ��������������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ʾ����ABCD�У�BC=x��CD=y��y��x����ķ�����������ϵ��ͼ2��ʾ������ֱ��������AEF��б��EF��C�㣬MΪEF���е㣬�����н�����ȷ����

A. ��x=3ʱ��EC��EM B. ��y=9ʱ��EC��EM
C. ��x����ʱ��EC��CF��ֵ���� D. ��y����ʱ��BE��DF��ֵ���䡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������
����һ�����һ���������ĸ�λ���ֵ��ڳ���λ����֮���������λ����֮�ͣ���������Ϊ���������������磺��1+2=3������123��������������ͬ����55��1315Ҳ��������������
���϶�������![]() ����λ��������������������x��2��x��x+2�ֱ���������İ�λ���֣�ʮλ���֣���λ���֣����磺135��468��Ϊ����������
����λ��������������������x��2��x��x+2�ֱ���������İ�λ���֣�ʮλ���֣���λ���֣����磺135��468��Ϊ����������
���⣺
��1����֪a����������������������������������b��b��0��ʹ10a+bΪһ����������������b����Сֵ��
��2����֪һ����λ����������![]() ��һ�������������ĺ��ܱ�3��������c��a+d��b=4��֤��
��һ�������������ĺ��ܱ�3��������c��a+d��b=4��֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ���䶥����ֱ��
���䶥����ֱ��![]() ��.
��.
��1����![]() ��ֵ;
��ֵ;
��2����![]() ���������;
���������;
��3����![]() Ϊһ���ڱ���
Ϊһ���ڱ���![]() �����
�����![]() ����
����![]() ��ĶԳƵ�
��ĶԳƵ�![]() �Ƿ��ڸ���������?
�Ƿ��ڸ���������?
��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������е��Ժ��������ٶȱ���������ѧ��ÿ�������뺺�ֵĸ������ռ���������±����� ��
�༶ | �μ����� | ��λ�� | ƽ���� | ���� |
�� | 55 | 149 | 135 | 191 |
�� | 55 | 151 | 135 | 110 |
ijͬѧ�����ϱ������ó����½��ۣ�
��1���ס�������ѧ���ɼ���ƽ��ˮƽ��ͬ��
��2���Ұ�������������ڼװ��������������ÿ�������뺺��![]() ��Ϊ���㣩
��Ϊ���㣩
��3���װ�ɼ��IJ���������Ұ�ɼ��IJ���С.
������������ȷ���ǣ� ��
A.��1����2����3��B.��1����2��C.��1����3��D.��2����3��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com