
【题目】在平面直角坐标系中,有两个点![]() ,
,![]() .
.
(1)若![]() 、
、![]() 关于
关于![]() 轴对称,则
轴对称,则![]() _________________,
_________________,![]() ________________.
________________.
(2)若![]() 、
、![]() 关于
关于![]() 轴对称,则
轴对称,则![]() _________________,
_________________,![]() ________________.
________________.
(3)若![]() 、
、![]() 两点重合,将重合后的点绕原点顺时针旋转
两点重合,将重合后的点绕原点顺时针旋转![]() ,此时点的坐标为__________.
,此时点的坐标为__________.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;
;![]() ;(3)
;(3)![]()
【解析】
(1)根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得答案;
(2)根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可得答案;
(3)根据旋转的性质,构造全等三角形求出边长可得答案.
解:(1)∵点A、B关于x轴对称,纵坐标互为相反数
∴x1=2,y2=5;
(2)∵点A、B关于y轴对称,横坐标互为相反数
∴x1=-2,y2=5;
(3)∵![]() 、
、![]() 两点重合,∴坐标合并为(2,-5),
两点重合,∴坐标合并为(2,-5),
如图,将点A绕原点顺时针旋转![]() 得到点A′,
得到点A′,
分别作点A和A′到x轴的垂线于点E、F,
由旋转的性质可知A′O=AO,
由同角的余角相等可知:∠A′OF=∠A,
在△AEO和△OFA′中,
 ,
,
∴△AEO≌△OFA′,
∴OE=A′F,AE=OF,
∴点A′的坐标为![]() .
.



科目:初中数学 来源: 题型:
【题目】数学兴趣小组几名同学到商场调查发现,一种纯牛奶进价为每箱40元,厂家要求售价在40~70元之间,若以每箱70元销售平均每天销售30箱,价格每降低1元平均每天可多销售3箱.
(1)现该商场要保证每天盈利900元,同时又要使顾客得到实惠,那么每箱售价为多少元?
(2)若每天盈利为W元,请利用配方法直接写出每箱售价为多少元时,每天盈利最多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,相交于点O,![]() cm,
cm,![]() cm,E,F分别是AB,BC的中点,点P是对角线AC上的一个动点,设
cm,E,F分别是AB,BC的中点,点P是对角线AC上的一个动点,设![]() cm,
cm,![]() cm,
cm,![]() cm
cm
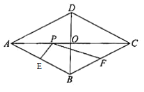
小明根据学习函数的经验,分别对这两种函数随自变量的变化而变化的情况进行了探究,下面是小明探究过程,请补充完整:
(1)画函数![]() 的图象
的图象
①按下表自变量的值进行取点、画图、测量,得到了![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 1.12 | 0.5 | 0.71 | 1.12 | 1.58 | 2.06 | 2.55 | 3.04 |
②在所给坐标系中描出补全后的表中的各对应值为坐标的点,画出函数![]() 的图象;
的图象;

(2)画函数![]() 的图象
的图象
在同一坐标系中,画出函数![]() 的图象;
的图象;
(3)根据画出的函数![]() 的图象、函数
的图象、函数![]() 的图象,解决问题
的图象,解决问题
①函数![]() 的最小值是________________;
的最小值是________________;
②函数![]() 的图象与函数
的图象与函数![]() 的图象的交点表示的含义是________________;
的图象的交点表示的含义是________________;
③若![]() ,AP的长约为________________cm
,AP的长约为________________cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位农民带上若干千克自产的苹果进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的苹果![]() (千克)与他手中持有的钱数
(千克)与他手中持有的钱数![]() (元)(含备用零钱)的关系如图,结合图象解决下列问题:
(元)(含备用零钱)的关系如图,结合图象解决下列问题:
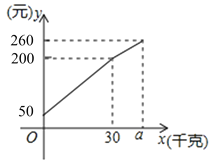
(1)农民自带的零钱是多少?
(2)求出降价前每千克的苹果价格是多少?
(3)降价后他按每千克![]() 元将剩余苹果售完,这时他手中
元将剩余苹果售完,这时他手中![]() 的钱(含备用零钱)是
的钱(含备用零钱)是![]() 元,试求出图象中
元,试求出图象中![]() 的值;
的值;
(4)求出降价前![]() 与
与![]() 之间的关系式(不要求写
之间的关系式(不要求写![]() 的取值范围).
的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
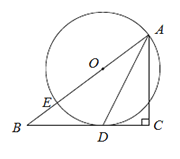
【题目】已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连结AD.
(1)求证:AD是∠BAC的平分线;
(2)若AC=3,BC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
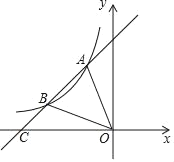
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 图象相交于点A(﹣1,2)与点B(﹣4,n).
图象相交于点A(﹣1,2)与点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
(3)在第二象限内,求不等式ax+b<![]() 的解集(请直接写出答案).
的解集(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).

(1)求步道的宽.
(2)为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.己知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2, 且区域丙为正方形,求塑胶跑道的总面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com