
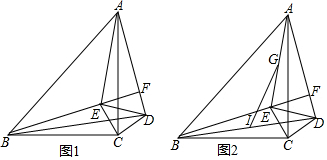
分析 (1)如图1中,设AC交BF于O.由△BCE≌△ACD推出BE=AD,∠CBE=∠CAD,由∠AOF=∠BOC,推出∠AFC=∠BCO=90°;
(2)结论:FE+FD=$\sqrt{2}$FC.由△CME≌△CND,推出CM=CM.EM=DN,推出四边形CMFN是正方形,推出FM=FN,CF=$\sqrt{2}$FM,由FE+FD=FM+EM+FN-DN=2FM,即可推出FE+FD=$\sqrt{2}$FC.
(3)如图3中,如图作EM⊥BC于M,EN⊥AC于N,则四边形EMCN是矩形,由S△ABC=S△ABE+S△ACE+S△BCE,可得8=6+$\frac{1}{2}$×4×EN+$\frac{1}{2}$×4×EM,推出EM+EN=1,由CM=1,EC=1,推出E与N重合,如图3中,易知CG=2.5,CI=1.5,在Rt△IGC中,根据IG=$\sqrt{C{I}^{2}+C{G}^{2}}$计算即可.
解答 (1)证明:如图1中,设AC交BF于O.
∵AC⊥BC,AC=BC,DC⊥EC,DC=EC,
∴∠BCA=∠ECD,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$,
∴△BCE≌△ACD,
∴BE=AD,∠CBE=∠CAD,
∵∠AOF=∠BOC,
∴∠AFC=∠BCO=90°,
∴BF⊥AD.
(2)解:结论:FE+FD=$\sqrt{2}$FC.
理由:作CM⊥BF于M,CN⊥AD于N.则四边形CMFN是矩形,
∴∠MCN=∠ECD=90°,
∴∠ECM=∠DCN,
∵CE=CD,∠CME=∠CND,
∴△CME≌△CND,
∴CM=CM.EM=DN,
∴四边形CMFN是正方形,
∴FM=FN,CF=$\sqrt{2}$FM,
∵FE+FD=FM+EM+FN-DN=2FM,
∴FE+FD=$\sqrt{2}$FC.
(3)如图2中,如图作EM⊥BC于M,EN⊥AC于N,则四边形EMCN是矩形,
∵S△ABC=S△ABE+S△ACE+S△BCE,
∴8=6+$\frac{1}{2}$×4×EN+$\frac{1}{2}$×4×EM,
∴EM+EN=1,
∵EC=1,
①当EM=1,
∴E与N重合,如图3中,易知CG=2.5,CI=1.5,
在Rt△IGC中,IG=$\sqrt{C{I}^{2}+C{G}^{2}}$=$\sqrt{2.{5}^{2}+1.{5}^{2}}$=$\frac{\sqrt{34}}{2}$.
②当EN=1时,E与M重合,此时GI=$\frac{3\sqrt{2}}{2}$.
点评 本题考查三角形综合题、等腰直角三角形的性质、全等三角形的判定和性质、正方形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
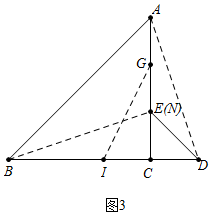
 爸爸为了检查小明对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.小明稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧.
爸爸为了检查小明对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.小明稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
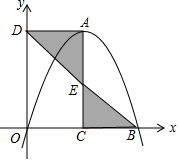 如图,在平面直角坐标系中,抛物线y=-x2+4x的顶点为A,与x轴分别交于O、B两点,过顶点A分别作AC⊥x轴于点C,AD⊥y轴于点D,连接BD,交AC于点E,则△ADE与△BCE的面积和为4.
如图,在平面直角坐标系中,抛物线y=-x2+4x的顶点为A,与x轴分别交于O、B两点,过顶点A分别作AC⊥x轴于点C,AD⊥y轴于点D,连接BD,交AC于点E,则△ADE与△BCE的面积和为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
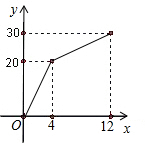 有一个附有进出水管的容器,每单位时间内进出的水量都是一定的,设从某时
有一个附有进出水管的容器,每单位时间内进出的水量都是一定的,设从某时查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com