
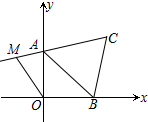
 如图所示,在平面直角坐标系中,A(0,3)、B(3,0)、C(4,4),线段CA的延长线上有一点M,使四边形ABOM的面积与三角形ABC的面积相等,则M的坐标为(-2,$\frac{5}{2}$).
如图所示,在平面直角坐标系中,A(0,3)、B(3,0)、C(4,4),线段CA的延长线上有一点M,使四边形ABOM的面积与三角形ABC的面积相等,则M的坐标为(-2,$\frac{5}{2}$). 分析 先过点C作CD⊥x轴与D,过点M作ME⊥AO于E,根据待定系数法求得直线AC解析式,再根据四边形ABOM的面积与三角形ABC的面积相等,求得点M的横坐标,最后根据直线解析式求得M的纵坐标即可.
解答 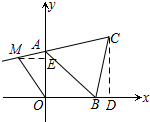 解:过点C作CD⊥x轴与D,过点M作ME⊥AO于E,
解:过点C作CD⊥x轴与D,过点M作ME⊥AO于E,
设直线AC解析式为y=kx+b,
∵A(0,3)、C(4,4),
∴$\left\{\begin{array}{l}{3=b}\\{4=4k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=3}\end{array}\right.$,
∴y=$\frac{1}{4}$x+3
∵A(0,3)、B(3,0)、C(4,4),
∴AO=3,BO=3,OD=4,CD=4,
∴四边形ABOM的面积
=△AOM的面积+△AOB的面积
=$\frac{1}{2}$×3×(ME+3)
=$\frac{3}{2}$(ME+3),
△ABC的面积
=梯形AODC的面积-△AOB的面积-△BCD的面积
=$\frac{(3+4)×4}{2}$-$\frac{1}{2}$×3×3-$\frac{1}{2}$×1×4
=14-$\frac{9}{2}$-2
=$\frac{15}{2}$,
∵四边形ABOM的面积与三角形ABC的面积相等,
∴$\frac{3}{2}$(ME+3)=$\frac{15}{2}$,
∴ME=2,即M的横坐标为-2,
当x=-2时,y=$\frac{1}{4}$×(-2)+3=$\frac{5}{2}$,
∴M(-2,$\frac{5}{2}$).
点评 本题主要考查了三角形的面积以及坐标与图形性质,解决问题的关键是掌握待定系数法以及三角形的面积计算公式,解题时注意方程思想运用.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:选择题
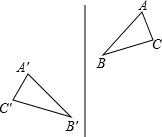 如图,把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换,你认为在滑动对称变换过程中,对应点不在变换直线上的两个对应三角形的对应点所具有的性质是( )
如图,把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换,你认为在滑动对称变换过程中,对应点不在变换直线上的两个对应三角形的对应点所具有的性质是( )| A. | 对应点连线与对称轴垂直 | B. | 对应点连线被对称轴平分 | ||
| C. | 对应点连线被对称轴垂直平分 | D. | 对应点连线互相平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32 | B. | 24 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com