Question

4．已知点F的坐标为（0，2），点M为x轴上一个动点，连接FM，作线段FM的垂直平分线l₁，过点M作x轴的垂线l₂，记l₁，l₂的交点为点P（x，y）．
（1）用含x的式子表示y；
（2）点A（x₁，y₁），B（x₂，y₂）在点P运动形成的图象上，且x₁＜x₂，能与点F构成等边三角形的点A，B有几对？请说明理由．

Answer 1

分析 （1）利用垂直平分线的性质建立方程化简即可；
（2）利用等边三角形的性质确定出直线AF解析式，联立方程组转化为一元二次方程，用根的判别式判断出有两个交点，即可．

解答 解：（1）如图1，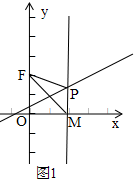

∵点P在FM的垂直平分线上，
∴PM=PF
∴$|y|=\sqrt{{x^2}+{{（y-2）}^2}}$
∴$y=\frac{1}{4}{x^2}+1$
（2）解：有2对，理由如下：
如图2，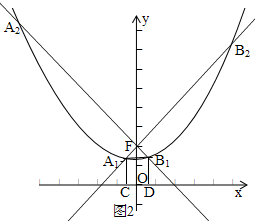

∵A，B在点P运动形成的图象上
过A，B作AC⊥x轴于C，BD⊥x轴于D
有（1）得FA=AC，FB=BD
若△FAB是等边三角形
∴FA=FB
∴AC=BD，
∴y₁=y₂，
∴AB∥x轴，
∵∠FAB=60°
∴直线AF解析式为y=$\sqrt{3}$x+2，
联立：$\left\{{\begin{array}{l}{y=\sqrt{3}x+2}\\{y=\frac{1}{4}{x^2}+1}\end{array}}\right.$
∴$\frac{1}{4}$x²-$\sqrt{3}$x-1=0，
∴△=（-$\sqrt{3}$）²-4×$\frac{1}{4}$×（-1）=4＞0，
∴该直线与抛物线有两个交点，如图交点即为A₁和B₂
其对称点分别为B₁和A₂，能与点F构成等边三角形的点A，B有且只有两对．

点评 此题是二次函数综合题，主要考查了垂直平分线的性质，等边三角形的性质，一元二次方程根的判别式，解本题的关键是确定出直线AF的解析式．