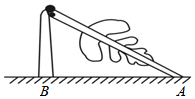
如图.一棵大树在一次强台风中距地面5m处折断.倒下后树顶端着地点A距树底端B的距离为12m.这棵大树在折断前的高度为( )A．10mB．15mC．18mD．20m 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

3．

如图，一棵大树在一次强台风中距地面5m处折断，倒下后树顶端着地点A距树底端B的距离为12m，这棵大树在折断前的高度为（　　）

A．

10m

B．

15m

C．

18m

D．

20m

分析根据大树的折断部分与未断部分、地面恰好构成直角三角形，再根据勾股定理求出AC的长，进而可得出结论．

解答解：∵树的折断部分与未断部分、地面恰好构成直角三角形，且BC=5m，AB=12m，
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13m，
∴这棵树原来的高度=BC+AC=5+13=18m．
即：这棵大树在折断前的高度为18m．
故选：C．

点评本题考查的是勾股定理的应用，熟知直角三角形斜边的平方等于两直角边的平方和是解答此题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

13．

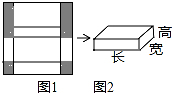如图1是边长为18cm的正方形纸板，截掉阴影部分后将其折叠成如图2所示的长方体盒子．已知该长方体的宽是高的2倍，则它的体积是216cm³．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

14．下列计算正确的是（　　）

A．

（ab）²=a²b²

B．

2a-a=2

C．

a²+a²=a⁴

D．

（a²）³=a⁵

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．暑期，某学校将组织部分优秀学生分别到A、B、C、D四个地方进行夏令营活动，学校按定额购买了前往四地的车票．如图1是未制作完成的车票种类和数量的条形统计图，请根据统计图回答下列问题：
（1）若去C地的车票占全部车票的30%，则去C地的车票数量是30 张，补全统计图；
（2）若学校采用随机抽取的方式分发车票，每人一张（所有车票的形状、大小、质地完全相同且充分洗匀），那么李明同学抽到去B地的概率是多少？
（3）若有一张去A地的车票，红红和天天都想要，决定采取旋转转盘的方式来确定．其中甲转盘被分成四等份且标有数字1、2、3、4，乙转盘分成三等份且标有数字7、8、9，如图2所示．具体规定是：同时转动两个转盘，当指针指向的两个数字之和是偶数时，票给红红，否则票给天天（指针指在线上重转）．试用“列表法”或“树状图”的方法分析这个规定对双方是否公平．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

18．已知：Rt△ABC中，AB=4，AC=3，则BC的长为$\sqrt{7}$或5．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．

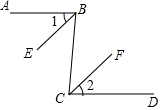填写下面证明过程中的推理依据：
已知：如图，AB∥CD，BE平分∠ABC，CF平分∠BCD．求证：∠1=∠2
证明：∵AB∥CD （已知）
∴∠ABC=∠BCD（两直线平行，内错角相等）
∵BE平分∠ABC，CF平分∠BCD （已知）
∴∠1=∠ABC，（角平分线的定义）
∠2=∠BCD．（角平分线的定义）
∴∠1=∠2．（等量代换）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．

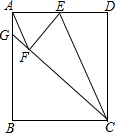如图，点E为矩形ABCD中AD边中点，将矩形ABCD沿CE折叠，使点D落在矩形内部的点F处，延长CF交AB于点G，连接AF．
（1）求证：AF∥CE；
（2）探究线段AF，EF，EC之间的数量关系，并说明理由；
（3）若BC=6，BG=8，求AF的长．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

12．已知二元一次方程3x-y=2，用关于x的代数式表示y为y=3x-2；当x=2时，y=4．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．如图，在正方形ABCD中，对角线AC与BD交于点O，在Rt△PFE中，∠EPF=90°，点E、F分别在边AD、AB上．
（1）如图1，若点P与点O重合：①求证：AF=DE；②若正方形的边长为2$\sqrt{3}$，当∠DOE=15°时，求线段EF的长；
（2）如图2，若Rt△PFE的顶点P在线段OB上移动（不与点O、B重合），当BD=3BP时，证明：PE=2PF．

查看答案和解析>>

同步练习册答案