
如图,Rt△ABC在平面直角坐标系中,BC在x轴上,B (-1,0)、A (0,2),AC⊥AB.

(1)求线段OC的长;
(2)点P从B点出发以每秒4个单位的速度沿x轴正半轴运动,点Q从A点出发沿线段AC以每秒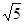 个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面
积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面
积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
(3)Q点沿射线AC按原速度运动,⊙G过A、B、Q三点,是否有这样的t值使点P在⊙G上、如果有求t值,如果没有说明理由.
(1)4(2)S=2t2-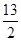 t+5(0<t<
t+5(0<t<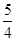 ),S=-2t2+
),S=-2t2+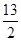 t-5(
t-5(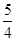 <t<2),t=
<t<2),t=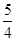 或t=2时C、P、Q都在同一直线上,S=0(3)当t=
或t=2时C、P、Q都在同一直线上,S=0(3)当t=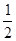 时,点P在圆G上
时,点P在圆G上
【解析】(1)∵AC⊥AB,
∴∠ABO+∠ACO=90°,
∵∠BAO+∠ABO=90°,
∴∠BAO=∠ACO∠ABO=∠COO,
∴△AOB∽△COA,
∴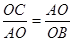
∵B(-1,0)、A(0,2),
∴OA=2,OB=1,
∴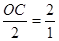 ,
,
∴OC=4;………………………………3分
(2)①当P在BC上,Q在线段AC上时,(0<t<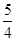 )过点Q作QD⊥BC于D,
)过点Q作QD⊥BC于D,
如图所示,则CQ=2 -
- t,CP=5-4t,
t,CP=5-4t,
由△CQD∽△CAO可得QD=2-t,
所以S=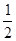 CP•QD=
CP•QD=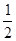 (5-4t)(2-t),
(5-4t)(2-t),
即S=2t2-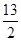 t+5(0<t<
t+5(0<t<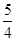 );………………………………5分
);………………………………5分
②当P在BC延长线上,Q在线段AC上时(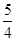 <t<2),过点Q作QD⊥BC于D,
<t<2),过点Q作QD⊥BC于D,
如图所示,则CQ=2 -
- t,CP=4t-5,
t,CP=4t-5,
由△CQD∽△CAO可得QD=2-t,
所以S=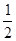 CP•QD=
CP•QD=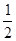 (4t-5)(2-t),
(4t-5)(2-t),
即S=-2t2+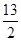 t-5(
t-5(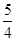 <t<2),………………………………7分
<t<2),………………………………7分
③当t=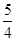 或t=2时C、P、Q都在同一直线上,S=0.………………………………8分
或t=2时C、P、Q都在同一直线上,S=0.………………………………8分
(3)若点P在圆G上,因为AC⊥AB,所以BQ是直径,所以∠BPQ=Rt∠,即PQ⊥BC,
则BP2+PQ2=BQ2=BA2+AQ2,
得|4t|2+|2-t|2=( )2+(
)2+( t)2,
t)2,
解得t1=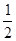 ,t2=-
,t2=-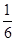 (不合题意,舍去)
(不合题意,舍去)
所以当t=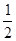 时,点P在圆G上.………………………………10分
时,点P在圆G上.………………………………10分
(也可以在(2)的基础上分类讨论,利用相似求得)

(1)利用△AOB∽△COA即可求得OC=4.
(2)分当P在BC上,Q在线段AC上时、当P在BC延长线上,Q在线段AC上时、当C、P、Q都在同一直线上利用△CQD∽△CAO求得t值即可.
(3)若点P在圆G上,因为AC⊥AB,所以BQ是直径,所以∠BPQ=Rt∠,即PQ⊥BC,则BP2+PQ2=BQ2=BA2+AQ2,得到有关t的式子求解即可.


科目:初中数学 来源: 题型:
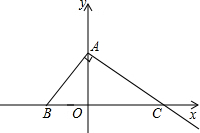 (2013•桥东区二模)如图,Rt△ABC在平面直角坐标系中,BC在x轴上,B(-1,0)、A(0,2),AC⊥AB.
(2013•桥东区二模)如图,Rt△ABC在平面直角坐标系中,BC在x轴上,B(-1,0)、A(0,2),AC⊥AB.| 5 |
查看答案和解析>>
科目:初中数学 来源:2012届河北省保定市易县九年级第一次模拟检测数学试卷(带解析) 题型:解答题
如图,Rt△ABC在平面直角坐标系中,BC在x轴上,B (-1,0)、A (0,2),AC⊥AB.
(1)求线段OC的长;
(2)点P从B点出发以每秒4个单位的速度沿x轴正半轴运动,点Q从A点出发沿线段AC以每秒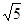 个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面 积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面 积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
(3)Q点沿射线AC按原速度运动,⊙G过A、B、Q三点,是否有这样的t值使点P在⊙G上、如果有求t值,如果没有说明理由.
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(四川南充) 题型:填空题
如图,Rt△ABC在第一象限, ,AB=AC=2,点A在直线
,AB=AC=2,点A在直线 上,其中点A的横坐标为1,且AB∥
上,其中点A的横坐标为1,且AB∥ 轴,AC∥
轴,AC∥ 轴,若双曲线
轴,若双曲线
 与△
与△ 有交点,则k的取值范围是 .
有交点,则k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(湖北荆门) 题型:填空题
如图,Rt△ABC在第一象限, ,AB=AC=2,点A在直线
,AB=AC=2,点A在直线 上,其中点A的横坐标为1,且AB∥
上,其中点A的横坐标为1,且AB∥ 轴,AC∥
轴,AC∥ 轴,若双曲线
轴,若双曲线
 与△
与△ 有交点,则k的取值范围是
.
有交点,则k的取值范围是
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com