
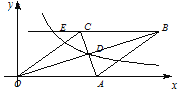
【题目】如图,在直角坐标系中,四边形 OABC 为菱形,对角线 OB、AC 相交于 D 点,已知 A点的坐标为(10,0),双曲线 y=![]() ( x>0 )经过 D 点,交 BC 的延长线于 E 点,且 OBAC=120(OB>AC),有下列四个结论:①双曲线的解析式为y=
( x>0 )经过 D 点,交 BC 的延长线于 E 点,且 OBAC=120(OB>AC),有下列四个结论:①双曲线的解析式为y=![]() (x>0);②E 点的坐标是(4,6);③sin∠COA=
(x>0);②E 点的坐标是(4,6);③sin∠COA=![]() ;④EC=
;④EC=![]() ;⑤AC+OB=8
;⑤AC+OB=8![]() .其中正确的结论有( )
.其中正确的结论有( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
【答案】A
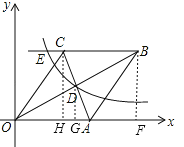
【解析】解:如图,过B作BF⊥x轴于点F,过D作DG⊥x轴于点G,过C作CH⊥x轴于点H.∵A(10,0),∴OA=10,∴S菱形ABCD=OABF=![]() ACOB=
ACOB=![]() ×120=60,即10BF=60,∴BF=6.在Rt△ABF中,AB=10,BF=8,由勾股定理可得AF=8,∴OF=OA+AF=10+8=18.∵四边形OABC为菱形,∴D为OB中点,∴DG=
×120=60,即10BF=60,∴BF=6.在Rt△ABF中,AB=10,BF=8,由勾股定理可得AF=8,∴OF=OA+AF=10+8=18.∵四边形OABC为菱形,∴D为OB中点,∴DG=![]() BF=
BF=![]() ×6=3,OG=
×6=3,OG=![]() OF=
OF=![]() ×18=9,∴D(9,3).∵双曲线过点D,∴3=
×18=9,∴D(9,3).∵双曲线过点D,∴3=![]() ,解得:k=27,∴双曲线解析式为y=
,解得:k=27,∴双曲线解析式为y=![]() ,故①正确;
,故①正确;
∵BC∥OF,BF=6,∴6=![]() ,x=
,x=![]() ,∴E(
,∴E(![]() ,6).故②错误;
,6).故②错误;
在Rt△OCH中,OC=10,CH=6,∴sin∠COA=![]() =
=![]() =
=![]() ,故③正确;
,故③正确;
∵C(8,6),E(![]() ,6),∴EC=8﹣
,6),∴EC=8﹣![]() =
=![]() ,故④正确.在Rt△OBF中,OF=18,BF=6,∴OB=
,故④正确.在Rt△OBF中,OF=18,BF=6,∴OB=![]() =6
=6![]() .∵ACOB=120,∴AC=
.∵ACOB=120,∴AC=![]() =2
=2![]() ,∴AC+OB=6
,∴AC+OB=6![]() +2
+2![]() =8
=8![]() ,故⑤正确;
,故⑤正确;
综上可知:正确的为①③④⑤共4个.故选A.


科目:初中数学 来源: 题型:
【题目】已知![]() 与
与![]() 成正比例,且
成正比例,且![]() 时,
时,![]() .
.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)将所得函数图象平移,使它过点(2, -1).求平移后直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
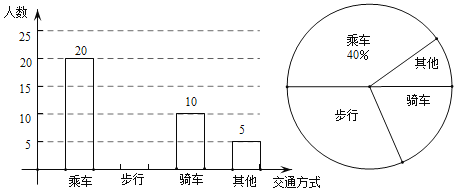
【题目】某学校为了解学生上学的交通方式,现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查,规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项,并将统计结果绘制了如下两幅不完整的统计图.
请解答下列问题:
(1)在这次调查中,该学校一共抽样调查了 名学生;
(2)补全条形统计图;
(3)若该学校共有1500名学生,试估计该学校学生中选择“步行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形A`B`C`是由三角形ABC经过某种平移得到的,点A与点A`,点B与点B`,点C与点C`分别对应,观察点与点坐标之间的关系,解答下列问题:

![]() 分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
![]() 若点
若点![]() 是点
是点![]() 通过
通过![]() 中的平移变换得到的,求
中的平移变换得到的,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是学习初中数学的- -个重要工具利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:数轴上点![]() 、点
、点![]() 表示的数为
表示的数为![]() ,则
,则![]() 两点之间的距离
两点之间的距离![]() ,若
,若![]() ,则可简化为;
,则可简化为;![]() 线段
线段![]() 的中点
的中点![]() 表示的数为
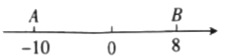
表示的数为![]() 如图,已知数轴上有
如图,已知数轴上有![]() 两点,分别表示的数为
两点,分别表示的数为![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度沿数轴向右匀速运动,点
个单位长度的速度沿数轴向右匀速运动,点![]() 以每秒
以每秒![]() 个单位长度向左匀速运动,设运动时间为
个单位长度向左匀速运动,设运动时间为![]() 秒
秒![]() .
.
(1)运动开始前,![]() 两点的距离为多少个单位长度;线段
两点的距离为多少个单位长度;线段![]() 的中点
的中点![]() 所表示的数为?
所表示的数为?
(2)点![]() 运动
运动![]() 秒后所在位置的点表示的数为 ;点
秒后所在位置的点表示的数为 ;点 ![]() 运动
运动![]() 秒后所在位置的点表示的数为 . (用含
秒后所在位置的点表示的数为 . (用含![]() 的式子表示)
的式子表示)
(3)它们按上述方式运动,![]() 两点经过多少秒会相距
两点经过多少秒会相距![]() 个单位长度?
个单位长度?
(4)若![]() 按上述方式运动,
按上述方式运动, ![]() 两点经过多少秒,线段
两点经过多少秒,线段![]() 的中点
的中点![]() 与原点重合?
与原点重合?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于
于![]() ,
,![]() 是
是![]() 的垂直平分线,点
的垂直平分线,点![]() 为垂足,
为垂足,![]() 的延长线与
的延长线与![]() 的延长线相交于点
的延长线相交于点![]() ,连结
,连结![]() ,已知
,已知![]() ,
,![]() ,则图中长为4的线段有( )
,则图中长为4的线段有( )
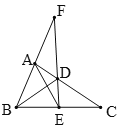
A. 5条B. 4条C. 3条D. 2条
查看答案和解析>>
科目:初中数学 来源: 题型:
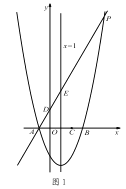
【题目】如图1,对称轴为直线x=1的抛物线y=![]() x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
(1)求点 B 的坐标和抛物线的表达式;
(2)当 AE:EP=1:4 时,求点 E 的坐标;
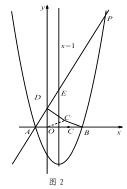
(3)如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到 OC ′,旋转角为 α(0°<α<90°),连接 C ′D、C′B,求 C ′B+ ![]() C′D 的最小值.
C′D 的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com