
分析 (1)由于一元二次方程x2+2(m+1)x+m2+5=0有两个实根x1,x2,于是得到△=[2(m+1)]2-4(m2+5)=4m2+8m+4-4m2-20=8m-16≥0,解不等式即可得到结论;
(2)当m=3时,方程可化为x2+8x+14=0,根据根与系数的关系得到x1+x2=-8,x1•x2=14,代入代数式即可得到结果;
(3)把根与系数的关系代入-x1-x2=-(x1+x2)=$\frac{2}{3}$x1•x2,解关于m的方程即可得到结果.
解答 解:(1)∵一元二次方程x2+2(m+1)x+m2+5=0有两个实根x1,x2,
∴△=[2(m+1)]2-4(m2+5)=4m2+8m+4-4m2-20=8m-16≥0,
解得:m≥2;
(2)当m=3时,方程可化为x2+8x+14=0,
∵x1+x2=-8,x1•x2=14,
∴x12+x22=(x1+x2)2-2x1x2=(-8)2-2×14=36,
所以斜边长6;
(3)-x1-x2=-(x1+x2)=$\frac{2}{3}$x1•x2,
∴2(m+1)=$\frac{2}{3}$(m2+5),
∴m1=1,m2=2,
又∵m≥2,
∴m=2.
点评 本题主要考查了根的判别式、因式分解法解一元二次方程、根与系数的关系以及勾股定理的知识,解答本题的关键是求出m的取值范围,此题难度一般.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
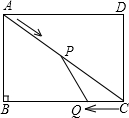 如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB项点B移动,设P、Q两点移动t秒(0<t<5)后,三角形CPQ的面积为S米2.
如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB项点B移动,设P、Q两点移动t秒(0<t<5)后,三角形CPQ的面积为S米2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
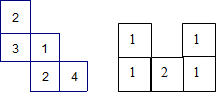 如图,这是一个由小立方块塔成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面、从左面看到的形状图.
如图,这是一个由小立方块塔成的几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.请你画出它从正面、从左面看到的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y3>y1>y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com