
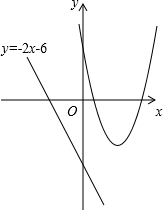
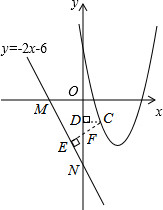
 (2013•柳州)已知二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),(5,0),(3,-4).
(2013•柳州)已知二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),(5,0),(3,-4).
|
|
| 5 |
| OM |
| ON |
| 1 |
| 2 |
| OM |
| MN |
| ||
| 5 |
| 1 |
| 2 |
| DF |
| sin∠DCF |
| DF |
| sin∠MNO |
| ||||
|
| ||
| 2 |
| 1 |
| 2 |
| ||
| 5 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 5 |
| 1 |
| 2 |
| ||
| 5 |
| ||
| 5 |
7
| ||
| 5 |
7
| ||
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
7
| ||
| 5 |
7
| ||
| 5 |
7
| ||
| 5 |


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
 (2013•柳州二模)已知:如图所示的一张矩形纸片ABCD,(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE,若AE=8cm,△ABF的面积为33cm,则△ABF的周长等于( )
(2013•柳州二模)已知:如图所示的一张矩形纸片ABCD,(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE,若AE=8cm,△ABF的面积为33cm,则△ABF的周长等于( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•柳州二模)已知:如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(2013•柳州二模)已知:如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:
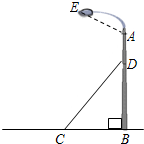 (2013•柳州二模)如图,一个钢结构支柱AB被钢缆CD固定于地面,已知DC=5米,sin∠DCB=
(2013•柳州二模)如图,一个钢结构支柱AB被钢缆CD固定于地面,已知DC=5米,sin∠DCB=| 3 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com