
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③![]() <a<
<a<![]() ;④b>c.其中含所有正确结论的选项是( )
;④b>c.其中含所有正确结论的选项是( )

A.①②③B.①③④C.②③④D.①②④
【答案】B
【解析】
根据对称轴为直线x=1及图象开口向下可判断出a、b、c的符号,从而判断①;根据对称性得到函数图象经过(3,0),则得②的判断;根据图象经过(-1,0)可得到a、b、c之间的关系,从而对④作判断;从图象与y轴的交点B在(0,-2)和(0,-1)之间可以判断c的大小得出③的正误.
①∵函数开口方向向上,
∴a>0;
∵对称轴在y轴右侧
∴ab异号,
∵抛物线与y轴交点在y轴负半轴,
∴c<0,
∴abc>0,
故①正确;
②∵图象与x轴交于点A(-1,0),对称轴为直线x=1,
∴图象与x轴的另一个交点为(3,0),
∴当x=2时,y<0,
∴4a+2b+c<0,
故②错误;
③∵图象与y轴的交点B在(0,-2)和(0,-1)之间,
∴-2<c<-1
∵-![]() ,
,
∴b=-2a,
∵函数图象经过(-1,0),
∴a-b+c=0,
∴c=-3a,
∴-2<-3a<-1,
∴![]() <a<
<a<![]() ;故③正确
;故③正确
④∵函数图象经过(-1,0),
∴a-b+c=0,
∴b-c=a,
∵a>0,
∴b-c>0,即b>c;
故④正确;
故选B.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象交反比例函数![]() 的图象于点A(2,﹣4)和点B(n,﹣2),交x轴于点C.
的图象于点A(2,﹣4)和点B(n,﹣2),交x轴于点C.
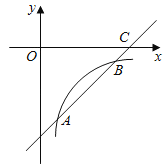
(1)求这两个函数的表达式;
(2)求△AOB的面积;
(3)请直接写出使一次函数值大于反比例函数值的x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
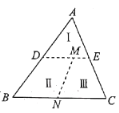
【题目】如图,现有一张三角形纸片![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 中点,点
中点,点![]() 是
是![]() 上一定点,点
上一定点,点![]() 是
是![]() 上一动点。将纸片依次沿
上一动点。将纸片依次沿![]() ,
,![]() 剪开,得到Ⅰ、Ⅱ和Ⅲ三部分,将Ⅱ绕点
剪开,得到Ⅰ、Ⅱ和Ⅲ三部分,将Ⅱ绕点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 重合,将Ⅲ绕点
重合,将Ⅲ绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 与
与![]() 重合,拼成了一个新的图形,则这个新图形周长的最小值是( )
重合,拼成了一个新的图形,则这个新图形周长的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
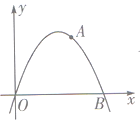
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 为抛物线上一点,且横纵坐标相等(原点除外),
为抛物线上一点,且横纵坐标相等(原点除外),![]() 为抛物线上一动点,过
为抛物线上一动点,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,并与直线
,并与直线![]() 交于点
交于点![]() .
.
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)当点![]() 在线段
在线段![]() 上方时,过
上方时,过![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() ,求
,求![]() 周长的最大值及此时
周长的最大值及此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推进素质教育,在初一年级设立了六个课外兴趣小组,如图是六个兴趣小组的频数分布直方图和扇形统计图,请根据图中提供的信息回答下列问题:
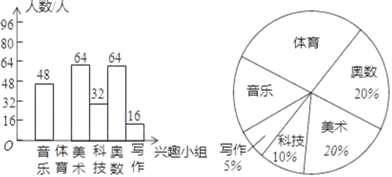
(1)初一年级共有多少人?
(2)补全频数分布直方图.
(3)求“从该年级中任选一名学生,是参加音乐、科技两个小组学生”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
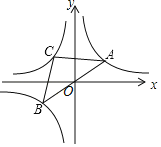
【题目】如图,已知A,B为反比例函数y1=![]() 图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=
图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=![]() (k<0)在第二象限内的图象上一点,当△CAB是以AB为底的等腰三角形,且
(k<0)在第二象限内的图象上一点,当△CAB是以AB为底的等腰三角形,且![]() 时,k的值为( )
时,k的值为( )
A.﹣![]() B.﹣3C.﹣4D.﹣
B.﹣3C.﹣4D.﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
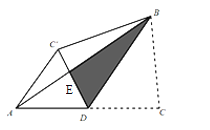
【题目】如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC′沿BD翻折,得到△![]() ,DC与AB交于点E,连结
,DC与AB交于点E,连结![]() ,若AD=AC′=2,BD=3则点D到BC的距离为( )
,若AD=AC′=2,BD=3则点D到BC的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
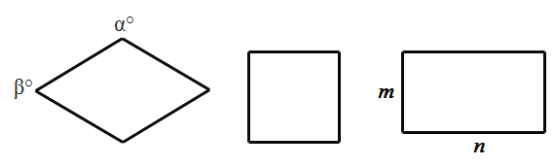
【题目】如图,我们规定菱形与正方形,矩形与正方形的接近程度称为“接近度”,在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为![]() ,
,![]() ,将菱形的“接近度”定义为
,将菱形的“接近度”定义为![]() ,于是
,于是![]() 越小,菱形越接近正方形.
越小,菱形越接近正方形.
①若菱形的一个内角为![]() ,则该菱形的“接近度”为_________;
,则该菱形的“接近度”为_________;
②当菱形的“接近度”等于_________时,菱形是正方形;
(2)设矩形的长和宽分别为![]() ,
,![]()
![]() ,试写出矩形的“接近度”的合理定义.
,试写出矩形的“接近度”的合理定义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com