
【题目】在△ABC中,点D在边BA或BA的延长线上,过点D作DE∥BC,交∠ABC的角平分线于点E.
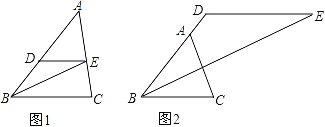
(1)如图1,当点D在边BA上时,点E恰好在边AC上,求证:∠ADE=2∠DEB;
(2)如图2,当点D在BA的延长线上时,请直接写出∠ADE与∠DEB之间的数量关系,并说明理由.
【答案】(1)详见解析;(2)∠ADE+2∠DEB=180°.
【解析】
(1)由角平分线的定义可得出∠ABE=∠CBE,由平行线的性质可得出∠CBE=∠DEB、∠ADE=∠ABC,进而可得出∠ABE=∠DEB,再利用三角形外角的性质即可证出∠ADE=2∠DEB;
(2)由角平分线的定义可得出∠ABC=2∠CBE,利用平行线的性质可得出∠DEB=∠CBE,进而可得出∠ABC=2∠DEB,再利用“两直线平行,同旁内角互补”可证出∠ADE+2∠DEB=180°.
证明:(1)∵BE平分∠ABC,
∴∠ABE=∠CBE.
∵DE∥BC,
∴∠CBE=∠DEB,∠ADE=∠ABC,
∴∠ABE=∠DEB,
∴∠ADE=∠ABE+∠DEB=2∠DEB.
(2)∠ADE+2∠DEB=180°.
∵BE平分∠ABC,
∴∠ABC=2∠CBE.
∵DE∥BC,
∴∠DEB=∠CBE,∠ADE+∠ABC=180°,
∴∠ABC=2∠DEB,
∴∠ADE+2∠DEB=180°.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】一只不透明的口袋中原来装有1个白球、2个红球,每个球除颜色外完全相同.则下列将袋中球增减的办法中,使得将球摇匀,从中任意摸出一个球,摸到白球与摸到红球的概率不相等为( )
A. 在袋中放入1个白球 B. 在袋中放入1个白球、2个红球
C. 在袋中取出1个红球 D. 在袋中放入2个白球、1个红球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,左面的几何体叫三棱柱,它有五个面,![]() 条棱,
条棱,![]() 个顶点,中间和右边的几何体分别是四棱柱和五棱柱.
个顶点,中间和右边的几何体分别是四棱柱和五棱柱.

![]() 四棱柱有________个顶点,________条棱,________个面;
四棱柱有________个顶点,________条棱,________个面;
![]() 五棱柱有________个顶点,________条棱,________个面;
五棱柱有________个顶点,________条棱,________个面;
![]() 你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
![]() 棱柱有几个顶点,几条棱,几个面吗?
棱柱有几个顶点,几条棱,几个面吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2017的直角顶点的坐标为.( ).

A. (4032,0) B. (4032,![]() ) C. (8064,0) D. (8052,
) C. (8064,0) D. (8052, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D在边BA或BA的延长线上,过点D作DE∥BC,交∠ABC的角平分线于点E.
(1)如图1,当点D在边BA上时,点E恰好在边AC上,求证:∠ADE=2∠DEB;
(2)如图2,当点D在BA的延长线上时,请直接写出∠ADE与∠DEB之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某班研究性学习小组在一次综合实践活动中发现如下问题:在楼底的B处测得河对岸大厦上悬挂的条幅底端D的仰角为26°,在楼顶A处测得条幅顶端C的仰角为50°.若楼AB高度为18米,条幅CD长度为46米,请你帮助他们求出楼与大厦之间的距离BE及大厦的高度CE.(参考数据:sin26°≈0.44,sin50°≈0.77,tan26°≈0.49,tan50°≈1.19).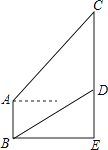
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )

A. 得分在70~80分之间的人数最多
B. 该班的总人数为40
C. 得分在90~100分之间的人数最少
D. 及格(≥60分)人数是26
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com