
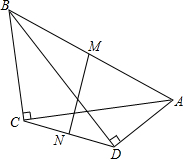
 如图,∠ACB=∠ADB=90°,M、N分别为AB、CD的中点.求证:MN⊥CD.
如图,∠ACB=∠ADB=90°,M、N分别为AB、CD的中点.求证:MN⊥CD. 科目:初中数学 来源: 题型:选择题
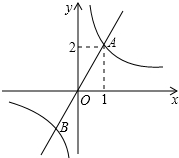 如图,函数y1=$\frac{{k}_{1}}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
如图,函数y1=$\frac{{k}_{1}}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )| A. | x>l | B. | -1<x<0 | C. | -l<x<0 或x>l | D. | x<-1 或 0<x<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB与AD,使他们分别落在角的两边上,过点A、C画一条射线AE,AE就是∠PRQ的平分线.试利用全等知识,说明角平分仪的画图原理.
如图:小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB与AD,使他们分别落在角的两边上,过点A、C画一条射线AE,AE就是∠PRQ的平分线.试利用全等知识,说明角平分仪的画图原理.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度p也随之改变,ρ与V在一定范围内满足ρ=$\frac{m}{v}$,它的图象如图所示,则该气体的质量m为( )
在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度p也随之改变,ρ与V在一定范围内满足ρ=$\frac{m}{v}$,它的图象如图所示,则该气体的质量m为( )| A. | 1.4kg | B. | 5kg | C. | 7kg | D. | 6.4kg |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com