
【题目】已知:如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
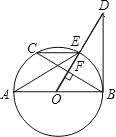
(1)求证:BD是⊙O的切线;
(2)当AB=10,BC=8时,求BD的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:从切线的判定为目标,来求BD⊥AB,连接AC通过相似来证得;通过已知条件和第一步求得的三角形相似求得BD的长度.
试题解析:(1)连接AC,
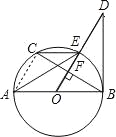
∵AB是⊙O的直径
∴∠ACB=90°
又∵OD⊥BC
∴AC∥OE
∴∠CAB=∠EOB
由![]() 对的圆周角相等
对的圆周角相等
∴∠AEC=∠ABC
又∵∠AEC=∠ODB
∴∠ODB=∠OBC
∴△DBF∽△OBD
∴∠OBD=90°
即BD⊥AB
又∵AB是直径
∴BD是⊙O的切线.
(2)∵OD⊥弦BC于点F,且点O圆心,
∴BF=FC
∴BF=4
由题意OB是半径即为5
∴在直角三角形OBF中OF为3
由以上(1)得到△DBF∽△OBD
∴![]()
即得BD=![]() .
.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
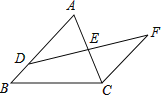
【题目】如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C作CF∥AB交DE延长线于点F.
(1)求证:AD=CF.
(2)连接AF,CD,求证:四边形ADCF为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
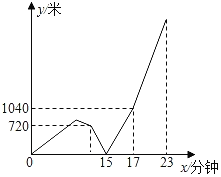
【题目】小刚从家出发匀速步行去学校上学.几分钟后发现忘带数学作业,于是掉头原速返回并立即打电话给爸爸,挂断电话后爸爸立即匀速跑步去追小刚,同时小刚以原速的两倍匀速跑步回家,爸爸追上小刚后以原速的![]() 倍原路步行回家.由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校,并在从家出发后23分钟到校(小刚被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小刚从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小刚家到学校的路程为_____米.
倍原路步行回家.由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校,并在从家出发后23分钟到校(小刚被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小刚从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小刚家到学校的路程为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
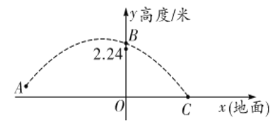
【题目】2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作,若将垫球后排球的运动路线近似的看作拋物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点![]() )离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点
)离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点![]() )越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点
)越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点![]() )距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )
)距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
数学活动课上,老师让同学们以“三角形的旋转”为主题开展数学活动,![]() 和
和![]() 是两个全等的直角三角形纸片,其中
是两个全等的直角三角形纸片,其中![]() ,
,![]() ,
,![]() .
.
解决问题
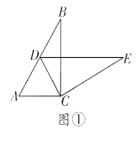
(1)如图①,智慧小组将![]() 绕点
绕点![]() 顺时针旋转,发现当点
顺时针旋转,发现当点![]() 恰好落在
恰好落在![]() 边上时,
边上时,![]() ,请你帮他们证明这个结论;
,请你帮他们证明这个结论;
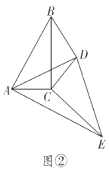
(2)缜密小组在智慧小组的基础上继续探究,连接![]() ,当
,当![]() C绕点
C绕点![]() 继续旋转到如图②所示的位置时,他们提出
继续旋转到如图②所示的位置时,他们提出![]() ,请你帮他们验证这一结论是否正确,并说明理由;
,请你帮他们验证这一结论是否正确,并说明理由;
探索发现
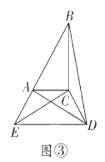
(3)如图③,勤奋小组在前两个小组的启发下,继续旋转![]() ,当
,当![]() 三点共线时,求
三点共线时,求![]() 的长;
的长;
(4)在图①的基础上,写出一个边长比为![]() 的三角形(可添加字母).
的三角形(可添加字母).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了了解我校七年级学生课外阅读的喜好,随机抽取我校七年级的部分学生进行问卷调查(每人只选一种书籍).下图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息回答问题:
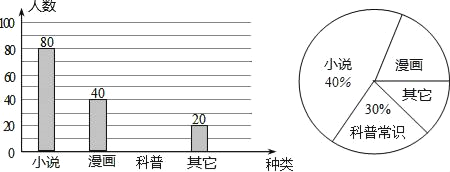
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,喜欢漫画的部分所占圆心角是 度;
(4)若七年级共有学生2800人,请你估计喜欢“科普常识”的学生人数共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图

根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,
(1)尺规作图:作AD平分∠BAC交BC于D点,再作AD的垂直平分线交AB于E点,交AC于F点(保留作图痕迹,不写作法);
(2)连接DE,DF证明:四边形AEDF是菱形;
(3)若BE=7,AF=4,CD=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
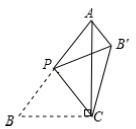
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的动点(不与点
边上的动点(不与点![]() 重合),将
重合),将![]() 沿
沿![]() 所在的直线翻折,得到
所在的直线翻折,得到![]() ,连接
,连接![]() ,则下列判断:
,则下列判断:
①当![]() 时,
时,![]()
②当![]() 时,
时,![]()
③当![]() 时,
时,![]() ;
;
④![]() 长度的最小值是1.
长度的最小值是1.
其中正确的判断是______(填入正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com