
°æƒø°ø–°’≈≥–∞¸¡À“ª∆¨ªƒ…Ω£¨À˚œÎ∞—’‚∆¨ªƒ…Ω∏ƒ‘Ï≥…“ª∏ˆ∆ªπ˚‘∞£¨œ÷‘⁄”–“ª÷÷∆ªπ˚ ˜√Á£¨À¸µƒ≥…ªÓ¬ »Áœ¬±ÌÀ˘ æ£∫
“∆÷≤ø√ ˝ | ≥…ªÓ ˝ | ≥…ªÓ¬ | “∆÷≤ø√ ˝ | ≥…ªÓ ˝ | ≥…ªÓ¬ |
50 | 47 |
| 1500 | 1335 |
|
270 | 235 |
| 3500 | 3203 |
|
400 | 369 |
| 7000 | 6335 |
|
750 | 662 |
| 14000 | 12628 |
|
œ¬√Ê”–Àƒ∏ˆÕ∆∂œ£∫
¢Ÿµ±“∆÷≤µƒ ˜ ˝ «1500 ±£¨±Ì∏Òº«¬º≥…ªÓ ˝ «1335£¨À˘“‘’‚÷÷ ˜√Á≥…ªÓµƒ∏≈¬ «![]() £ª
£ª
¢⁄ÀÊ◊≈“∆÷≤ø√ ˝µƒ‘ˆº”£¨ ˜√Á≥…ªÓµƒ∆µ¬ ◊Б⁄![]() ∏ΩΩ¸∞⁄∂Ø£¨œ‘ æ≥ˆ“ª∂®µƒŒ»∂®–‘£¨ø…“‘π¿º∆ ˜√Á≥…ªÓµƒ∏≈¬ «
∏ΩΩ¸∞⁄∂Ø£¨œ‘ æ≥ˆ“ª∂®µƒŒ»∂®–‘£¨ø…“‘π¿º∆ ˜√Á≥…ªÓµƒ∏≈¬ «![]() £ª
£ª
¢€»Ù–°’≈“∆÷≤10000ø√’‚÷÷ ˜√Á£¨‘Úø…ƒÐ≥…ªÓ9000ø√£ª
¢Ð»Ù–°’≈“∆÷≤20000ø√’‚÷÷ ˜√Á£¨‘Ú“ª∂®≥…ªÓ18000ø√£Æ
∆‰÷–∫œ¿Ìµƒ «![]() °°°°
°°°°![]()
A. ¢Ÿ¢€B. ¢Ÿ¢ÐC. ¢⁄¢€D. ¢⁄¢Ð
°æ¥∞∏°øC
°æΩ‚Œˆ°ø
ÀÊ◊≈“∆÷≤ø√ ˝µƒ‘ˆº”£¨ ˜√Á≥…ªÓµƒ∆µ¬ ◊Б⁄![]() ∏ΩΩ¸∞⁄∂Ø£¨œ‘ æ≥ˆ“ª∂®µƒŒ»∂®–‘£¨ø…“‘π¿º∆ ˜√Á≥…ªÓµƒ∏≈¬ «
∏ΩΩ¸∞⁄∂Ø£¨œ‘ æ≥ˆ“ª∂®µƒŒ»∂®–‘£¨ø…“‘π¿º∆ ˜√Á≥…ªÓµƒ∏≈¬ «![]() £¨æð¥ÀΩ¯––≈–∂œº¥ø…£Æ
£¨æð¥ÀΩ¯––≈–∂œº¥ø…£Æ
Ω‚£∫![]() µ±“∆÷≤µƒ ˜ ˝ «1 500 ±£¨±Ì∏Òº«¬º≥…ªÓ ˝ «1 335£¨’‚÷÷ ˜√Á≥…ªÓµƒ∏≈¬ ≤ª“ª∂® «
µ±“∆÷≤µƒ ˜ ˝ «1 500 ±£¨±Ì∏Òº«¬º≥…ªÓ ˝ «1 335£¨’‚÷÷ ˜√Á≥…ªÓµƒ∏≈¬ ≤ª“ª∂® «![]() £¨π ¥ÌŒÛ£ª
£¨π ¥ÌŒÛ£ª
![]() ÀÊ◊≈“∆÷≤ø√ ˝µƒ‘ˆº”£¨ ˜√Á≥…ªÓµƒ∆µ¬ ◊Б⁄
ÀÊ◊≈“∆÷≤ø√ ˝µƒ‘ˆº”£¨ ˜√Á≥…ªÓµƒ∆µ¬ ◊Б⁄![]() ∏ΩΩ¸∞⁄∂Ø£¨œ‘ æ≥ˆ“ª∂®µƒŒ»∂®–‘£¨ø…“‘π¿º∆ ˜√Á≥…ªÓµƒ∏≈¬ «
∏ΩΩ¸∞⁄∂Ø£¨œ‘ æ≥ˆ“ª∂®µƒŒ»∂®–‘£¨ø…“‘π¿º∆ ˜√Á≥…ªÓµƒ∏≈¬ «![]() £¨π ’˝»∑£ª
£¨π ’˝»∑£ª
![]() »Ù–°’≈“∆÷≤10 000ø√’‚÷÷ ˜√Á£¨‘Úø…ƒÐ≥…ªÓ9 000ø√£¨π ’˝»∑£ª
»Ù–°’≈“∆÷≤10 000ø√’‚÷÷ ˜√Á£¨‘Úø…ƒÐ≥…ªÓ9 000ø√£¨π ’˝»∑£ª
![]() »Ù–°’≈“∆÷≤20 000ø√’‚÷÷ ˜√Á£¨‘Ú≤ª“ª∂®≥…ªÓ18 000ø√£¨π ¥ÌŒÛ£Æ
»Ù–°’≈“∆÷≤20 000ø√’‚÷÷ ˜√Á£¨‘Ú≤ª“ª∂®≥…ªÓ18 000ø√£¨π ¥ÌŒÛ£Æ
π —°£∫C£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ ‘≠–Õ£∫‘⁄Õº¢Ÿµƒæÿ–ŒMNPQ÷–£¨µ„E°¢F°¢G°¢H∑÷±‘⁄NP°¢PQ°¢QM°¢MN…œ£¨»Ù°œ1=°œ2=°œ3=°œ4£¨‘Ú≥∆Àƒ±þ–ŒEFGHŒ™æÿ–ŒMNPQµƒ∑¥…‰Àƒ±þ–Œ£Æ
≤Ÿ◊˜”ÎÃΩæø£∫‘⁄Õº¢⁄£¨Õº¢€µƒæÿ–ŒABCD÷–£¨AB=4£¨BC=8µ„E°¢F∑÷±‘⁄BC°¢CD±þ…œ£¨ ‘¿˚”√’˝∑Ω–ŒÕ¯∏Ò∑÷±◊˜≥ˆ¡ΩÕº÷–æÿ–ŒABCDµƒ∑¥…‰Àƒ±þ–ŒEFGH£¨≤¢«Û≥ˆ√ø∏ˆ∑¥…‰Àƒ±þ–ŒEFGHµƒ÷Ð≥§£Æ
∑¢œ÷”Δ¶”√£∫”…«∞√ʵƒ≤Ÿ◊˜ø…“‘∑¢œ÷“ª∏ˆæÿ–Œ”–≤ªÕ¨µƒ∑¥…‰Àƒ±þ–Œ£¨«“’‚–©∑¥…‰Àƒ±þ–Œµƒ÷Ð≥§∂ºœýµ»£¨»Ù‘⁄Õº¢Ÿæÿ–ŒMNPQ÷–£¨MN=3£¨NP=4‘Ú∆‰∑¥…‰Àƒ±þ–ŒEFGHµƒ÷Ð≥§Œ™°°°°£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
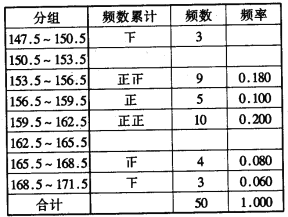
°æƒø°øŒ™¡À¡ÀΩ‚÷–—ß…˙µƒ…ÌÃÂ∑¢”˝«Èøˆ£¨∂‘ƒ≥“ª÷–—ßÕ¨ƒÍ¡‰µƒ50√˚≈Æ—ß…˙µƒ…Ì∏þΩ¯––¡À≤‚¡ø£¨Ω·π˚»Áœ¬(µ•Œª£∫¿Â√◊)£∫

ÕÍ≥…œ¬√ʵƒ∆µ¬ ∑÷≤º±Ì£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨”–“ª∏ˆø…“‘◊‘”…◊™∂صƒ◊™≈ñª∆Ωæ˘∑÷≥…3∏ˆ…»–Œ£¨∑÷±±Í”–1°¢2°¢3»˝∏ˆ ˝◊÷£¨–°Õı∫Õ–°¿Ó∏˜◊™∂Ø“ª¥Œ◊™≈ÃŒ™“ª¥Œ”Œœ∑£¨µ±√ø¥Œ◊™≈ÃÕ£÷π∫Û£¨÷∏’ÎÀ˘÷∏…»–Œƒ⁄µƒ ˝Œ™∏˜◊‘À˘µ√µƒ ˝£¨“ª¥Œ”Œœ∑Ω· ¯µ√µΩ“ª◊È ˝£®»Ù÷∏’Î÷∏‘⁄∑÷ΩÁœþ ±÷ÿ◊™£©£Æ
£®1£©«Îƒ„”√ ˜◊¥ÕºªÚ¡–±Ìµƒ∑Ω∑®±Ì æ≥ˆ√ø¥Œ”Œœ∑ø…ƒÐ≥ˆœ÷µƒÀ˘”–Ω·π˚£ª
£®2£©«Û√ø¥Œ”Œœ∑Ω· ¯µ√µΩµƒ“ª◊È ˝«°∫√ «∑Ω≥Ãx2©Å3x+2=0µƒΩ‚µƒ∏≈¬ £Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø¥”º◊µÿµΩ““µÿµƒª≥µ‘≠¿¥µƒ∆Ωæ˘ÀŸ∂» «100«ß√◊√ø–° ±£¨æ≠π˝¡Ω¥ŒÃ·ÀŸ∫Û∆Ωæ˘ÀŸ∂»Œ™121«ß√◊√ø–° ±£¨’‚¡Ω¥ŒÃ·ÀŸµƒ∞Ÿ∑÷¬ œýÕ¨£Æ
£®1£©«Û∏√ª≥µ√ø¥ŒÃ·ÀŸµƒ∞Ÿ∑÷¬ £ª
£®2£©»Ùº◊““¡ΩµÿÃ˙¬∑≥§220«ß√◊£¨«Ûµ⁄“ª¥ŒÃ·ÀŸ∫Û¥”º◊µÿµΩ““µÿÀ˘”√µƒ ±º‰±»Ã·ÀŸ«∞…Ÿ”√¡À∂ý…Ÿ–° ±£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø![]() ≥þπÊ◊˜Õº1£∫
≥þπÊ◊˜Õº1£∫
“—÷™£∫»ÁÕº£¨œþ∂ŒAB∫Õ÷±œþ«“µ„B‘⁄÷±œþ…œ
«Û◊˜£∫µ„C£¨ πµ„C‘⁄÷±œþ…œ≤¢«“ π![]() Œ™µ»—¸»˝Ω«–Œ£Æ
Œ™µ»—¸»˝Ω«–Œ£Æ
◊˜Õº“™«Û£∫±£¡Ù◊˜Õº∫€º££¨≤ª–¥◊˜∑®£¨◊ˆ≥ˆÀ˘”–∑˚∫œÃıº˛µƒµ„C£Æ
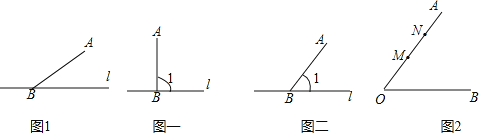
![]() Ãÿ¿˝Àºøº£∫
Ãÿ¿˝Àºøº£∫
»ÁÕº“ª£¨µ±![]() ±£¨∑˚∫œ
±£¨∑˚∫œ![]() ÷–Ãıº˛µƒµ„C”–______∏ˆ£ª»ÁÕº∂˛£¨µ±
÷–Ãıº˛µƒµ„C”–______∏ˆ£ª»ÁÕº∂˛£¨µ±![]() ±£¨∑˚∫œ
±£¨∑˚∫œ![]() ÷–Ãıº˛µƒµ„C”–______∏ˆ
÷–Ãıº˛µƒµ„C”–______∏ˆ![]()
![]() Õÿ’𔶔√£∫
Õÿ’𔶔√£∫
»ÁÕº£¨![]() £¨µ„M£¨N‘⁄…‰œþOA…œ£¨
£¨µ„M£¨N‘⁄…‰œþOA…œ£¨![]() £¨
£¨![]() £¨µ„P «…‰œþOB…œµƒµ„
£¨µ„P «…‰œþOB…œµƒµ„![]() »Ù πµ„P£¨M£¨Nππ≥…µ»—¸»˝Ω«–Œµƒµ„P”–«“÷ª”–»˝∏ˆ£¨«Ûxµƒ÷µ£Æ
»Ù πµ„P£¨M£¨Nππ≥…µ»—¸»˝Ω«–Œµƒµ„P”–«“÷ª”–»˝∏ˆ£¨«Ûxµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
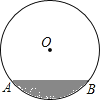
°æƒø°ø‘⁄∞Îæ∂Œ™17dmµƒ‘≤÷˘–Œ”ÕπÞƒ⁄◊∞Ω¯“ª–©”Õ∫Û£¨∫·Ωÿ√Ê»ÁÕº£Æ
£®1£©»Ù”Õ√ÊøÌAB=16dm£¨«Û”Õµƒ◊Ó¥Û…Ó∂»£Æ
£®2£©‘⁄£®1£©µƒÃıº˛œ¬£¨»Ù”Õ√Êø̱‰Œ™CD=30dm£¨«Û”Õµƒ◊Ó¥Û…Ó∂»…œ…˝¡À∂ý…Ÿdm£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨∂‘”⁄∆Ω√Ê…œ≤ª¥Û”⁄![]() µƒ
µƒ![]() £¨Œ“√«∏¯≥ˆ»Áœ¬∂®“£∫»Ùµ„P‘⁄
£¨Œ“√«∏¯≥ˆ»Áœ¬∂®“£∫»Ùµ„P‘⁄![]() µƒƒ⁄≤øªÚ±þΩÁ…œ£¨◊˜
µƒƒ⁄≤øªÚ±þΩÁ…œ£¨◊˜![]() ”⁄µ„E£¨£Æ
”⁄µ„E£¨£Æ![]() ”⁄µ„
”⁄µ„![]() £¨‘Ú≥∆
£¨‘Ú≥∆![]() Œ™µ„Pœý∂‘”⁄
Œ™µ„Pœý∂‘”⁄![]() µƒ°∞”≈µ„æý¿Î°±£¨º«Œ™
µƒ°∞”≈µ„æý¿Î°±£¨º«Œ™![]()

»ÁÕº2£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨∂‘”⁄![]() £¨µ„PŒ™µ⁄“ªœÛœÞƒ⁄ªÚ¡ΩÃı◊¯±Í÷·’˝∞Î÷·…œµƒ∂ص„£¨«“¬˙◊„
£¨µ„PŒ™µ⁄“ªœÛœÞƒ⁄ªÚ¡ΩÃı◊¯±Í÷·’˝∞Î÷·…œµƒ∂ص„£¨«“¬˙◊„![]() 5£¨µ„P‘À∂Ø–Œ≥…µƒÕº–Œº«Œ™Õº–ŒG£Æ
5£¨µ„P‘À∂Ø–Œ≥…µƒÕº–Œº«Œ™Õº–ŒG£Æ
£®1£©¬˙◊„Ãıº˛µƒ∆‰÷–“ª∏ˆµ„Pµƒ◊¯±Í « __£¨Õº–ŒG”Î◊¯±Í÷·Œß≥…Õº–Œµƒ√ʪ˝µ»”⁄ __ £ª
£®2£©…ËÕº–ŒG”Îx÷·µƒπ´π≤µ„Œ™µ„A£¨»ÁÕº3£¨“—÷™![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3£©»Áπ˚≈◊ŒÔœþ![]() æ≠π˝£®2£©÷–µƒA£¨B¡Ωµ„£¨µ„Q‘⁄A£¨B¡Ωµ„÷ƺ‰µƒŒÔœþ…œ£®µ„Qø…”ÎA£¨B¡Ωµ„÷ÿ∫œ£©£¨«Ûµ±
æ≠π˝£®2£©÷–µƒA£¨B¡Ωµ„£¨µ„Q‘⁄A£¨B¡Ωµ„÷ƺ‰µƒŒÔœþ…œ£®µ„Qø…”ÎA£¨B¡Ωµ„÷ÿ∫œ£©£¨«Ûµ±![]() »°◊Ó¥Û÷µ ±£¨µ„Q µƒ◊¯±Í£Æ
»°◊Ó¥Û÷µ ±£¨µ„Q µƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘ƒ∂¡œ¬¡–¡Ω‘Ú≤ƒ¡œ£¨ªÿ¥Œ £∫
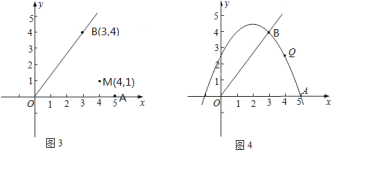
≤ƒ¡œ“ª£∫∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨∂‘µ„A£®x1£¨y1£©£¨B£®x2£¨y2£©∂®““ª÷÷–¬µƒ‘ÀÀ„£∫AB=x1x2+y1y2£Æ
¿˝»Á£∫»ÙA£®1£¨2£©£¨B£®3£¨4£©£¨‘ÚAB=1°¡3+2°¡4=11
≤ƒ¡œ∂˛£∫∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨π˝∫·◊¯±Í≤ªÕ¨µƒ¡Ωµ„A£®x1£¨y1£©£¨B£®x2£¨y2£©µƒ÷±œþµƒ–±¬ Œ™kAB=![]() £Æ”…¥Àø…“‘∑¢œ÷»ÙkAB=
£Æ”…¥Àø…“‘∑¢œ÷»ÙkAB=![]() =1£¨‘Ú”–y1-y2=x1-x2£¨º¥x1-y1=x2-y2£Æ∑¥÷Æ£¨»Ùx1£¨x2£¨y1£¨y2¬˙◊„πÿœµ Ωx1-y1=x2-y2£¨‘Ú”–y1-y2=x1-x2£¨ƒ«√¥kAB=
=1£¨‘Ú”–y1-y2=x1-x2£¨º¥x1-y1=x2-y2£Æ∑¥÷Æ£¨»Ùx1£¨x2£¨y1£¨y2¬˙◊„πÿœµ Ωx1-y1=x2-y2£¨‘Ú”–y1-y2=x1-x2£¨ƒ«√¥kAB=![]() ®T1£Æ
®T1£Æ
£®1£©“—÷™µ„M£®-4£¨6£©£¨N£®3£¨2£©£¨‘ÚMN=______£¨»Ùµ„A£¨Bµƒ◊¯±Í∑÷±Œ™£®x1£¨y1£©£¨£®x2£¨y2£©£®x1°Ÿx2£©£¨«“¬˙◊„πÿœµ Ωx1+y1=x2+y2£¨ƒ«√¥kAB=______£ª
£®2£©∫·◊¯±Íª•≤ªœýÕ¨µƒ»˝∏ˆµ„C£¨D£¨E¬˙◊„CD=DE£¨«“Dµ„µƒ◊¯±ÍŒ™£®2£¨2£©£¨π˝µ„D◊˜DF°Œy÷·£¨Ωª÷±œþCE”⁄µ„F£¨»ÙDF=8£¨«ÎΩ·∫œÕºœÛ£¨«Û÷±œþCE”Î◊¯±Í÷·Œß≥…µƒ»˝Ω«–Œµƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com