
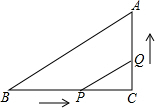
 如图所示,∠C=90°,BC=8cm,AC=6cm,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似?
如图所示,∠C=90°,BC=8cm,AC=6cm,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似? 分析 设经过y秒后相似,由于没有说明对应角的关系,所以共有两种情况:△CPQ∽△CBA与△CPQ∽△CAB
解答 解:设经过y秒后,△CPQ∽△CBA,此时BP=2y,CQ=y.
∵CP=BC-BP=8-2y,CB=8,CQ=y,CA=6.
∵△CPQ∽△CBA,
∴$\frac{CP}{CB}=\frac{CQ}{CA}$,
∴$\frac{8-2y}{8}=\frac{y}{6}$
∴y=2.4
设经过y秒后,△CPQ∽△CAB,此时BP=2y,CQ=y.
∴CP=BC-BP=8-2y.
∵△CPQ∽△CAB,
∴$\frac{CP}{CA}=\frac{CQ}{CB}$
∴$\frac{8-2y}{6}=\frac{y}{8}$
∴y=$\frac{32}{11}$
所以,经过2.4秒或者经过$\frac{32}{11}$后两个三角形都相似
点评 本题考查相似三角形的判定,解题的关键是分两种情况进行讨论,本题属于中等题型.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
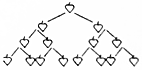 如图是一副“苹果图”,第一行有1个苹果,第二行有2个苹果,第三行有4个苹果,第四行有8个苹果…,猜猜第十行有29个苹果,第2017行有22016个苹果.
如图是一副“苹果图”,第一行有1个苹果,第二行有2个苹果,第三行有4个苹果,第四行有8个苹果…,猜猜第十行有29个苹果,第2017行有22016个苹果.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com