
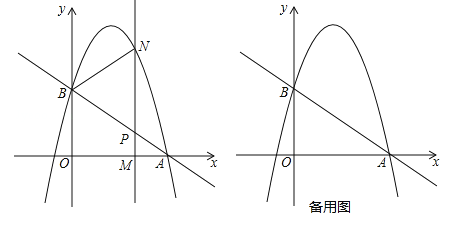
【题目】如图,抛物线y=﹣![]() +bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)在对称轴的左侧是否存在点M使四边形OMPB的面积最大,如果存在求点M的坐标;不存在请说明理由.
【答案】(1)AB的解析式为y=﹣![]() x+2,抛物线解析式为y=﹣
x+2,抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;(2)N点坐标为(
x+2;(2)N点坐标为(![]() );(3)不存在.
);(3)不存在.
【解析】试题分析:(1)用待定系数法分别求出直线AB的解析式和抛物线的解析式即可;(2)根据题意可得N(m,﹣![]() m2+
m2+![]() m+2),P(m,﹣
m+2),P(m,﹣![]() m+2),即可得NP=﹣
m+2),即可得NP=﹣![]() m2+4m,PM=﹣
m2+4m,PM=﹣![]() m+2,再由NP=PM,可得方程﹣
m+2,再由NP=PM,可得方程﹣![]() m2+4m=﹣
m2+4m=﹣![]() m+2,解方程即可求得m的值,从而求得点N的坐标;(3)在对称轴的左侧不存在点M使四边形OMPB的面积最大,根据题意和已知条件求出S梯形OMPB和m的函数关系式,利用二次函数的性质判定即可.
m+2,解方程即可求得m的值,从而求得点N的坐标;(3)在对称轴的左侧不存在点M使四边形OMPB的面积最大,根据题意和已知条件求出S梯形OMPB和m的函数关系式,利用二次函数的性质判定即可.
试题解析:
(1)设直线AB的解析式为y=px+q,
把A(3,0),B(0,2)代入得![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣![]() x+2;
x+2;
把A(3,0),B(0,2)代入y=﹣![]() +bx+c得
+bx+c得 ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)∵M(m,0),MN⊥x轴,
∴N(m,﹣![]() m2+
m2+![]() m+2),P(m,﹣
m+2),P(m,﹣![]() m+2),
m+2),
∴NP=﹣![]() m2+4m,PM=﹣
m2+4m,PM=﹣![]() m+2,
m+2,
而NP=PM,
∴﹣![]() m2+4m=﹣
m2+4m=﹣![]() m+2,解得m1=3(舍去),m2=
m+2,解得m1=3(舍去),m2=![]() ,
,
∴N点坐标为(![]() ,
,![]() );
);
(3)在对称轴的左侧不存在点M使四边形OMPB的面积最大,理由如下:
B(0,2),M(m,0),MN⊥x轴,
∴P(m,﹣![]() m+2),
m+2),
S梯形OMPB=![]() (PM+OB)OM=
(PM+OB)OM=![]() (﹣
(﹣![]() m+2+2)m
m+2+2)m
=﹣![]() m2+2m
m2+2m
=﹣![]() (m﹣3)2+3
(m﹣3)2+3
∵对称轴是x=﹣![]() =
=![]() ,M在对称轴的左侧,
,M在对称轴的左侧,
∴0<m<![]() ,
,
∴m的值无法确定,
在对称轴的左侧不存在点M使四边形OMPB的面积最大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( ).
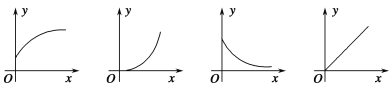
①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A.①②④③ B.③④②①
C.①④②③ D.③②④①
查看答案和解析>>
科目:初中数学 来源: 题型:
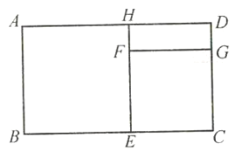
【题目】如图,长方形![]() 中,长
中,长![]() ,宽
,宽![]() ,四边形
,四边形![]() 和四边形
和四边形![]() 都是正方形.
都是正方形.
(1)求四边形![]() 的面积(用含
的面积(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)当![]() 、
、![]() 满足什么等量关系时,图形是一个轴对称图形.
满足什么等量关系时,图形是一个轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的边长为![]() ,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
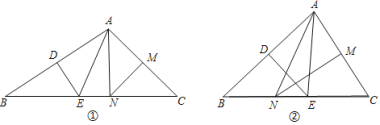
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
⑴如图①,若![]() ,求
,求![]() 的度数;
的度数;
⑵如图②,若![]() ,求
,求![]() 的度数;
的度数;
⑶若![]()
![]() ,直接写出用
,直接写出用![]() 表示
表示![]() 大小的代数式.
大小的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一个种植总面积为![]() 的矩形塑料温棚,分垄间隔套种草莓和西红柿共
的矩形塑料温棚,分垄间隔套种草莓和西红柿共![]() 垄,种植的草莓或西红柿单种农作物的总垄数不低于8垄,又不超过
垄,种植的草莓或西红柿单种农作物的总垄数不低于8垄,又不超过![]() 垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
⑴若设草莓共种植了![]() 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?
⑵在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
占地面积(m2/垄) | 产量(千克/垄) | 利润(元/千克) | |
西红柿 | 32 | 160 | 1.0 |
草莓 | 15 | 50 | 1.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明最喜欢吃芝麻馅的汤圆了,一天早晨小明妈妈给小明下了四个大汤圆,一个花生馅,一个水果馅,两个芝麻馅,四个汤圆除内部馅料不同外,其他一切均相同.
(1)求小明吃第一个汤圆恰好是芝麻馅的概率;
(2)请利用树状图或列表法,求小明吃前两个汤圆恰好是芝麻馅的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com