
【题目】下列全国各地地铁标志图中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
【答案】C
【解析】解:A、不是轴对称图形,也不是中心对称图形.故错误;
B、不是轴对称图形,是中心对称图形.故错误;
C、是轴对称图形,也是中心对称图形.故正确;
D、是轴对称图形,不是中心对称图形.故错误.
所以答案是:C.
【考点精析】利用轴对称图形和中心对称及中心对称图形对题目进行判断即可得到答案,需要熟知两个完全一样的图形关于某条直线对折,如果两边能够完全重合,我们就说这两个图形成轴对称,这条直线就对称轴;如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称;如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形.


科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,山坡斜面CD与水平面夹角为30°,坡面上点E处有一亭子,测得假山坡脚C与楼房水平距离BC=10米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.求楼房AB的高(结果保留根号).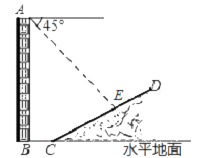
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】原题呈现:若a2+b2+4a﹣2b+5=0,求a、b的值.
方法介绍:
①看到a2+4a可想到如果添上常数4恰好就是a2+4a+4=(a+2)2,这个过程叫做“配方”,同理b2﹣2b+1=(b﹣1)2,恰好把常数5分配完;
②从而原式可以化为(a+2)2+(b﹣1)2=0由平方的非负性可得a+2=0且b﹣1=0.
经验运用:
(1)若4a2+b2﹣20a+6b+34=0,求a+b的值.
(2)若a2+5b2+c2﹣2ab﹣4b+6c+10=0,求a+b+c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式从左到右的变形,是因式分解的是()
A.x2-9+6x=(x+3)(x-3)+6xB.(x+5)(x-2)=x2+3x-10
C.x2-8x+16=(x-4)2D.x2+1=x(x+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的一次函数,当x=1时,y=1;当x=-2时,y=-14.
(1)求这个一次函数的关系式;
(2)在如图所示的平面直角坐标系中作出函数的图像;
(3)由图像观察,当0≤x≤2时,函数y的取值范围.
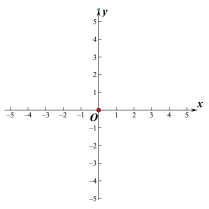
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】智能折叠电动车是在传统电动车的基础上,根据消费者需求生产的一种新型电动车.某智能折叠电动车公司计划每周生产1400辆,平均每天生产200辆.由于各种原因实际每天生产量与计划每天生产量相比有出入.下表是某周智能折叠电动车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆)

星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
生产情况 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产智能折叠电动车_______辆;
(2)产量最多的一天比产量最少的一天多生产________辆;
(3)若该公司实行按生产的智能折叠电动车数量的多少计工资,即计件工资制.如果每生产一辆智能折叠电动车可得人民币60元,那么该公司工人这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两组同学玩“两人背夹球”比赛,即:每组两名同学用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲组两位同学掉了球;乙组两位同学顺利跑完.设比赛中同学距出发点的距离用y表示,单位是米;比赛时间用x表示,单位是秒.两组同学比赛过程用图像表示如下:
(1)这是一次 米的背夹球比赛;
(2)线段 表示甲组两位同学在比赛中途掉球,耽误了 秒;
(3)甲组同学到达终点用了 秒,乙组同学到达终点用了 秒,获胜的是 组同学;
(4)请直接写出C点坐标,并说明点C的实际意义.
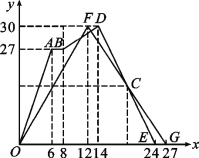
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某公司租用两种型号的货车各一辆,分別将产品运往甲市与乙市(运费收费标准如下表),已知该公司到乙市的距离比到甲市的距离远30km,B车的总运费比A车的总运费少1080元.
(1)求这家公司分别到甲、乙两市的距离;
(2)若A,B两车同时从公司出发,其中B车以60km/h的速度匀速驶向乙市,而A车根据路况需要,先以45kmh的速度行驶了3小吋,再以75km/h的速度行驹到达甲市.
①在行驶的途中,经过多少时间,A,B两车到各自目的地的距离正好相等?
②若公司希望B车能与A车同吋到达目的地,B车必须在以60km/h的速度行驶一段时间后提速,若提速后的速度为70km/h(速度从60km/h提速到70km/h的时间忽略不汁),则B车应该在行驶 小时后提速.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇想测量位于池塘两端的A,B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A,B两点的距离.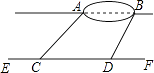
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com