
【题目】如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是__.
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.
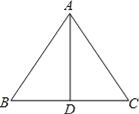
【答案】②③④
【解析】解:应添加的条件是②③④;
证明:②当∠BAD=∠CAD时,∵AD是∠BAC的平分线,且AD是BC边上的高,则△ABD≌△ACD,∴△BAC是等腰三角形;
③延长DB至E,使BE=AB;延长DC至F,使CF=AC;连接AE、AF.
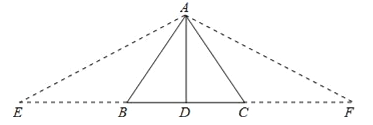
∵AB+BD=CD+AC,∴DE=DF,又AD⊥BC,∴△AEF是等腰三角形,∴∠E=∠F.
∵AB=BE,∴∠ABC=2∠E.
同理,得∠ACB=2∠F,∴∠ABC=∠ACB,即AB=AC,△ABC是等腰三角形;
④△ABC中,AD⊥BC,根据勾股定理,得:
AB2﹣BD2=AC2﹣CD2,即(AB+BD)(AB﹣BD)=(AC+CD)(AC﹣CD).
∵AB﹣BD=AC﹣CD①,∴AB+BD=AC+CD②;
∴①+②得:2AB=2AC,∴AB=AC,∴△ABC是等腰三角形.
故答案为:②③④.


科目:初中数学 来源: 题型:
【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种圆环(如图),它的外圆直径是8厘米,环宽1厘米.
①如果把这样的2个圆环扣在一起并拉紧(如图2),长度为___________厘米;
②如果用x个这样的圆环相扣并拉紧,长度为y厘米,则y与x之间的关系式是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F. 
(1)求证:四边形ABCD是正方形;
(2)当AE=2EF时,判断FG与EF有何数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活中,有人喜欢把传送的便条折成“![]() ”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
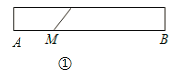

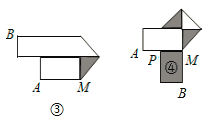
如果由信纸折成的长方形纸条(图①)长为2 6 厘米,分别回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点M与点A的距离为3厘米,那么在图②中,BE=_____厘米; 在图④中,BM=______厘米.
(2)如果长方形纸条的宽为x厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(结果用x表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外阅读是提高学生素养的重要途径,亚光初中为了了解学校学生的阅读情况,组织调查组对全校三个年级共1500名学生进行了抽样调查,抽取的样本容量为300.已知该校有初一学生600名,初二学生500名,初三学生400名. 
(1)为使调查的结果更加准确地反映全校的总体情况,应分别在初一年级随机抽取人;在初二年级随机抽取人;在初三年级随机抽取人.(请直接填空)
(2)调查组对本校学生课外阅读量的统计结果分别用扇形统计图和频数分布直方图表示如下请根据上统计图,计算样本中各类阅读量的人数,并补全频数分布直方图.
(3)根据(2)的调查结果,从该校中随机抽取一名学生,他最大可能的阅读量是多少本?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.
已知:如图,![]() 与
与![]() 互补,
互补,![]() ,
,
求证:![]()

证明:![]() 与
与![]() 互补
互补
即![]() ,(已知)
,(已知)
![]() // ( )
// ( )
![]() .( )
.( )
又![]() ,(已知)
,(已知)
![]() ,即
,即![]() .(等式的性质)
.(等式的性质)
![]() // (内错角相等,两直线平行)
// (内错角相等,两直线平行)
![]() .( )
.( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com