
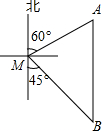
 如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.
如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.分析 (1)作AC⊥AB于C,根据余弦的定义计算;
(2)利用余弦的定义求出AM,计算即可.
解答 解:(1)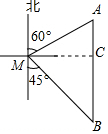 作AC⊥AB于C,
作AC⊥AB于C,
则MC=BM×cos45°=60$\sqrt{2}$海里,
答:渔船从B到A的航行过程中与码头M之间的最小距离为60$\sqrt{2}$海里;
(2)在Rt△ACM中,AM=$\frac{MC}{cos30°}$=40$\sqrt{6}$,
40$\sqrt{6}$÷20=2$\sqrt{6}$,
答:渔船从A到达码头M的航行时间为2$\sqrt{6}$小时.
点评 本题考查的是解直角三角形的应用-方向角问题以及勾股定理的应用,正确标注方向角、熟记锐角三角函数的定义是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=2 | B. | x=-2 | C. | x=$\frac{1}{2}$ | D. | x=-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在菱形ABCD中,对角线AC和BD交于点O,分别过点B、C作BE∥AC,CE∥BD,BE与CE交于点E.
如图,在菱形ABCD中,对角线AC和BD交于点O,分别过点B、C作BE∥AC,CE∥BD,BE与CE交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB∥CD,EF∥MN,∠1=115°.
如图,已知AB∥CD,EF∥MN,∠1=115°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com