
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
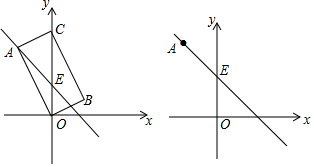
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 接通电源后的时间x (单位:min) | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | … |
| 水箱中水的温度y (单位:℃) | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | … |
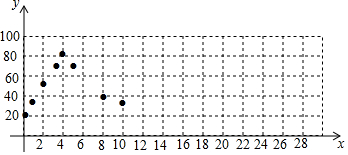
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
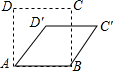 如图,若将长度相等的四根木条钉成的正方形木框ABCD变形成菱形ABC′D′的形状,并使∠BAD′=45°,则正方形ABCD的面积与菱形ABC′D′的面积之比为$\sqrt{2}$:1.
如图,若将长度相等的四根木条钉成的正方形木框ABCD变形成菱形ABC′D′的形状,并使∠BAD′=45°,则正方形ABCD的面积与菱形ABC′D′的面积之比为$\sqrt{2}$:1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com