
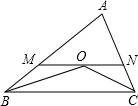
 如图,△ABC中,∠ABC、∠ACB的平分线相交于O,MN过点O且与BC平行.△ABC的周长为20,△AMN的周长为12,则BC的长为( )
如图,△ABC中,∠ABC、∠ACB的平分线相交于O,MN过点O且与BC平行.△ABC的周长为20,△AMN的周长为12,则BC的长为( )| A. | 10 | B. | 16 | C. | 8 | D. | 4 |
分析 由BO为角平分线,得到一对角相等,再由MN平行于BC,利用两直线平行内错角相等,得到一对角相等,等量代换可得出∠MBO=∠MOB,利用等角对等边得到MO=MB,同理得到NO=NC,而三角形ABC的周长等于三边相加,即AB+BC+AC,其中AB=AM+MB,AC=AN+NC,等量代换后可得出三角形ABC的周长等于三角形AMN的周长与BC的和,即BC等于两三角形的周长之差,将两三角形的周长代入,即可求出BC的长.
解答 解:∵OB平分∠MBC,
∴∠MBO=∠OBC,
又MN∥BC,
∴∠MOB=∠OBC,
∴∠MOB=∠MBO,
∴MB=MO,
同理可得∠NOC=∠NCO,
∴NO=NC,
∴(AB+AC+BC)-(AM+AN+MN)
=(AM+MB+AN+NC+BC)-(AM+AN+MN)
=(AM+MO+AN+NO+BC)-(AM+AN+MN)
=(AM+AN+MN+BC)-(AM+AN+MN)
=BC,
又∵△ABC的周长为20,△AMN的周长为12,即AB+AC+BC=20,AM+AN+MN=12,
则BC=20-12=8.
故选C.
点评 此题考查了等腰三角形的判定与性质,以及平行线的性质,利用了转化及等量代换的思想,熟练掌握判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中A点的坐标为(-3,0).
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中A点的坐标为(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形的中线、角平分线、高线都是线段 | |
| B. | 任意三角形的内角和都是180° | |
| C. | 三角形的三个角可以同时大于60° | |
| D. | 三角形的三条高至少有一条高在三角形的内部 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=CD,AD=BC | B. | AB∥CD,AD=BC | C. | AB∥CD,AD∥BC | D. | ∠A=∠C,∠B=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正面朝上的概率大 | B. | 反面朝上的概率大 | ||
| C. | 正面朝上和反面朝上的概率一样大 | D. | 一定是反面朝上 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com