
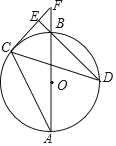
【题目】已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.如果∠ACB=75°,圆O的半径为2,则BD的长为_____.
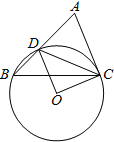
【答案】2.
【解析】
接OB,根据∠DOC=2∠ACD=90°.得∠ACD=45°,进而得∠BCD=30°,∠BOC=150°,∠DOB=60°,证明△BOD是等边三角形,即可求得BD的长.
如图,连接OB,
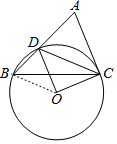
∵∠DOC=2∠ACD=90°.
∴∠ACD=45°,
∵∠ACB=75°,
∴∠BCD=∠ACB﹣∠ACD=30°,
∵OC=OD,∠DOC=90°,
∴∠DCO=45°,
∴∠BCO=∠DCO﹣∠BCD=15°,
∵OB=OC,
∴∠CBO=∠BCO=15°,
∴∠BOC=150°,
∴∠DOB=∠BOC﹣∠DOC=150°﹣90°=60°,
∵OB=OD,
∴△BOD是等边三角形,
∴BD=OD=2.
故答案为2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
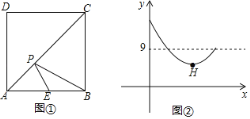
【题目】如图①,在正方形ABCD中,点E是AB的中点,点P是对角线AC上一动点,设PC的长度为x,PE与PB的长度和为y,图②是y关于x的函数图象,则图象上最低点H的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
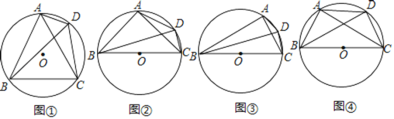
【题目】(1)方法选择:如图①,四边形ABCD是⊙O的内接四边形,连接AC,BD,AB=BC=AC.求证:BD=AD+CD.
小颖认为可用截长法证明:在DB上截取DM=AD,连接AM…
小军认为可用补短法证明:延长CD至点N,使得DN=AD…
请你选择一种方法证明.
(2)类比探究:(探究1)如图②,四边形ABCD是⊙O的内接四边形,连接AC,BD,BC是⊙O的直径,AB=AC.试用等式表示线段AD,BD,CD之间的数量关系,井证明你的结论.
(探究2)如图③,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,∠ABC=30°,则线段AD,BD,CD之间的等量关系式是 .
(3)拓展猜想:如图④,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,BC:AC:AB=a:b:c,则线段AD,BD,CD之间的等量关系式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】澜鑫商场为“双十一购物节”请甲乙两个广告公司布置展厅,已知乙单独完成此项任务的天数是甲单独完成此任务天数的2倍.若两公司合作4天,再由甲公司单独做3天就可以完成任务.
(1)甲公司与乙公司单独完成这项任务各需多少天?
(2)甲公司每天所需费用为5万元,乙公司每天所需费用为2万元,要使这项工作的总费用不超过40万元,则甲公司至多工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.
(1)求证:CF是⊙O的切线;
(2)当BD=![]() ,sinF=
,sinF=![]() 时,求OF的长.
时,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2m+1)x+m2﹣4=0有两个不相等的实数根
(1)求实数m的取值范围;
(2)若两个实数根的平方和等于15,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:千帕)随气体体积V(单位:立方米)的变化而变化,p随V的变化情况如表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出一个符合表格数据的p关于V的函数解析式
(2)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数解析式,基于安全考虑,气球的体积至少为多少立方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com