
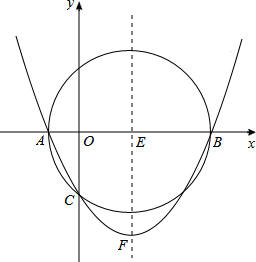 (2013•岳阳)如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F.
(2013•岳阳)如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F. 解:(1)∵以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,
解:(1)∵以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,| CE2-OE2 |
| 52-32 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 25 |
| 4 |
| 25 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| 41 |
| 41 |
| 41 |
| 41 |
| 1 |
| 4 |
| 3 |
| 2 |
| 41 |
| 41 |
| MG2+EG2 |
| 32+42 |
| 25 |
| 4 |
| 25 |
| 4 |
| 9 |
| 4 |
| MG2+FG2 |
32+(
|
| 15 |
| 4 |
| 15 |
| 4 |
| 25 |
| 4 |


科目:初中数学 来源: 题型:
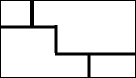 (2013•岳阳)夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为
(2013•岳阳)夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•岳阳)如图,反比例函数y=
(2013•岳阳)如图,反比例函数y=| k | x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com