练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．（1）计算：$\sqrt{12}+{（{π-2015}）^0}+{（\frac{1}{2}）^{-1}}$-6tan30°；
    （2）用配方法解方程：x2-4x-4=0．

    分析 （1）原式第一项化为最简二次根式，第二项利用零指数幂法则计算，第三项利用负整数指数幂法则计算，最后一项利用特殊角的三角函数值计算即可得到结果；
    （2）方程利用配方法求出解即可．

    解答 解：（1）原式=2$\sqrt{3}$+1+2-2$\sqrt{3}$=3；
    （2）配方，得（x-2）2=8，
    解得：x1=2+2$\sqrt{2}$，x2=2-2$\sqrt{2}$．

    点评 此题考查了实数的运算，以及解一元二次方程-配方法，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．如图，把一块含有30°的三角板的两个顶点放在一长方形纸片的对边上．如果∠1=20°，那么∠2的度数是40度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

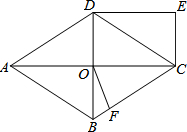    5．如图，菱形ABCD中，对角线AC、BD交于O点，DE∥AC，CE∥BD．
    （1）求证：四边形OCED为矩形；
    （2）在BC上截取CF=CO，连接OF，若AC=16，BD=12，求四边形OFCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图1和图2，△ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足是D，AE平分∠BAD，交BC于点E．过点A作AF⊥AE，过点C作CF∥AD，两直线交于点F．
    （1）在图1中，证明：△ACF≌△ABE；
    （2）在图2中，∠ACB的平分线交AB于点M，交AD于点N．
    ①求证：四边形ANCF是平行四边形；
    ②求证：ME=MA；
    ③四边形ANCF是不是菱形？若是，请证明；若不是，请简要说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列运算正确的是（　　）
    A．3a+3b=6abB．a3-a=a2C．a6÷a3=a2D．（a2）3=a6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．（1）解方程：x2-4x=0
    （2）化简：m（m+3）-（m+1）2，其中m=$\sqrt{2}$+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

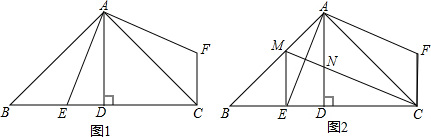
    6．如图，为测量某楼AB的高度，工作人员在点D处高1.8m的测角仪CD测得楼顶端A的仰角为30°，向前走40m到点E，又测得点A的仰角为60°，求楼AB的高度．（最后结果取近似值，保留两位小数，参考数据$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

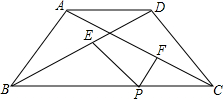    3．如图，在等腰梯形ABCD中，AD∥BC，AB=CD=3，P是BC上一点，PE∥CD交BD于点E，PF∥AB交AC于点F，设PE、PF的长分别是m、n，且x=m+n，那么当P在BC上移动时，x的值是否变化？若变化，求出x的取值范围；若不变，求出x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．某校七年级“启航班”的同学在老师带领下学习“数学活动”，步骤如下：
    （1）将全班同学分成几组，每组三人，合作完成本次数学活动．
    （2）每三人小组分别测试1分钟跳绳的次数并对照得分表换算成得分．
    （3）老师从中抽查了一个小组甲、乙、丙同学的得分数据，让同学们绘制成折线统计图．
    （4）根据折线统计图（图1）填写下表：

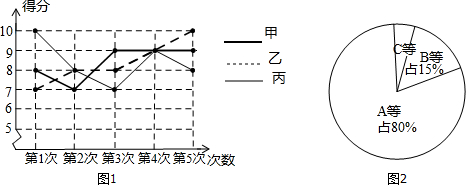
    平均数众 数中位数方 差综合评价
    甲8.4990.64成绩较为稳定的学生是甲．
    乙8.4881.04
    丙8.481.04
    （5）用测试统计的数据制成扇形统计图（图2）可知：跳绳成绩A等的学生占80%，在扇形图中所占圆心角为288度，B等的学生占15%，C等的学生有2人，占5%，参加跳绳的学生共有40人．

    查看答案和解析>>

    同步练习册答案